www.siteթույլ է տալիս գտնել. Կայքը կատարում է հաշվարկը: Մի քանի վայրկյանից սերվերը կտա ճիշտ լուծումը։ Մատրիցայի բնորոշ հավասարումըկլինի հանրահաշվական արտահայտություն, որը գտնվել է որոշիչի հաշվարկման կանոնի միջոցով մատրիցներ մատրիցներ, մինչդեռ հիմնական անկյունագծի երկայնքով տարբերություններ կլինեն անկյունագծային տարրերի և փոփոխականի արժեքների մեջ: Հաշվարկելիս բնորոշ հավասարում մատրիցայի համար առցանց, յուրաքանչյուր տարր մատրիցներկբազմապատկվի համապատասխան այլ տարրերով մատրիցներ. Գտեք ռեժիմում առցանցհնարավոր է միայն քառակուսի համար մատրիցներ. Գործողության որոնում բնորոշ հավասարում մատրիցայի համար առցանցնվազեցնում է տարրերի արտադրյալի հանրահաշվական գումարի հաշվարկը մատրիցներորոշիչը գտնելու արդյունքում մատրիցներ, միայն որոշելու նպատակով բնորոշ հավասարում մատրիցայի համար առցանց. Այս օպերացիան հատուկ տեղ է գրավում տեսության մեջ մատրիցներ, թույլ է տալիս գտնել սեփական արժեքներ և վեկտորներ՝ օգտագործելով արմատները: Գտնելու խնդիրը բնորոշ հավասարում մատրիցայի համար առցանցբաղկացած է բազմապատկվող տարրերից մատրիցներորին հաջորդում է այս ապրանքների ամփոփումը որոշակի կանոնի համաձայն. www.siteգտնում է մատրիցայի բնորոշ հավասարումըտրված չափը ռեժիմում առցանց. Հաշվարկ բնորոշ հավասարում մատրիցայի համար առցանցհաշվի առնելով դրա չափը՝ սա թվային կամ խորհրդանշական գործակիցներով բազմանդամ գտնելն է, որը գտնվել է ըստ որոշիչի հաշվարկման կանոնի։ մատրիցներ- որպես համապատասխան տարրերի արտադրյալների գումար մատրիցներ, միայն որոշելու նպատակով բնորոշ հավասարում մատրիցայի համար առցանց. Քառակուսի համար փոփոխականի նկատմամբ բազմանդամ գտնելը մատրիցներ, որպես սահմանում մատրիցայի բնորոշ հավասարումը, տեսականորեն տարածված մատրիցներ. Բազմանդամի արմատների նշանակությունը բնորոշ հավասարում մատրիցայի համար առցանցօգտագործվում է սեփական վեկտորները և սեփական արժեքները որոշելու համար մատրիցներ. Ընդ որում, եթե որոշիչը մատրիցներկամք հավասար է զրոյի, Դա մատրիցայի բնորոշ հավասարումըդեռ գոյություն կունենա՝ ի տարբերություն հակառակի մատրիցներ. Հաշվարկելու համար մատրիցայի բնորոշ հավասարումըկամ գտնել միանգամից մի քանիսը մատրիցների բնորոշ հավասարումներ, դուք պետք է շատ ժամանակ և ջանք ծախսեք, մինչդեռ մեր սերվերը կգտնի վայրկյանների ընթացքում բնորոշ հավասարում մատրիցների համար առցանց. Այս դեպքում գտնելու պատասխանը բնորոշ հավասարում մատրիցայի համար առցանցկլինի ճիշտ և բավարար ճշգրտությամբ, նույնիսկ եթե թվերը գտնելիս բնորոշ հավասարում մատրիցայի համար առցանցիռացիոնալ կլինի. Կայքում www.siteնիշերի մուտքերը թույլատրվում են տարրերում մատրիցներ, այսինքն բնորոշ հավասարում մատրիցների համար առցանցհաշվարկելիս կարելի է ներկայացնել ընդհանուր սիմվոլիկ ձևով առցանց մատրիցայի բնորոշ հավասարումը. Օգտակար է ստուգել ստացված պատասխանը գտնելու խնդիրը լուծելիս բնորոշ հավասարում մատրիցայի համար առցանցօգտագործելով կայքը www.site. Բազմանդամի հաշվարկման գործողություն կատարելիս. մատրիցայի բնորոշ հավասարումը, այս խնդիրը լուծելիս պետք է զգույշ և չափազանց կենտրոնացած լինել։ Իր հերթին, մեր կայքը կօգնի ձեզ ստուգել ձեր որոշումը թեմայի վերաբերյալ առցանց մատրիցայի բնորոշ հավասարումը. Եթե ​​ժամանակ չունեք լուծված խնդիրների երկար ստուգումների համար, ապա www.siteանշուշտ հարմար գործիք կլինի գտնելու և հաշվարկելիս ստուգելու համար բնորոշ հավասարում մատրիցայի համար առցանց.

Հրահանգներ

K թիվը կոչվում է A մատրիցի սեփական արժեք (թիվ), եթե կա x այնպիսի վեկտոր, որ Ax=kx: (1) Այս դեպքում x վեկտորը կոչվում է A մատրիցայի սեփական վեկտոր, որը համապատասխանում է k թվին R^n տարածության մեջ (տե՛ս նկ. 1), A մատրիցը ունի պատկերի ձևը:

Անհրաժեշտ է առաջադրանք դնել A մատրիցի վեկտորները գտնելու համար: X սեփական վեկտորը տրվի կոորդինատներով: Մատրիցային ձևով այն գրվելու է որպես սյունակային մատրիցա, որը հարմարության համար պետք է ներկայացվի որպես փոխադրված տող: X=(x1,x2,…,xn)^T Հիմնվելով (1), Ax-khx=0 կամ Ax-kEx=0 վրա, որտեղ E-ն նույնականացման մատրիցն է (գլխավոր անկյունագծի վրա գտնվողները, մնացած բոլոր տարրերը զրո են: ) Այնուհետև (A-kE)x=0: (2)

Գծային միատարր հանրահաշվական հավասարումների արտահայտությունը (2) ունի ոչ զրոյական լուծում (սեփական վեկտոր): Ուստի (2) համակարգի հիմնական որոշիչը հավասար է զրոյի, այսինքն՝ |A-kE|=0: (3) K սեփական արժեքի վերջին հավասարությունը կոչվում է A մատրիցի բնորոշ հավասարում և ընդլայնված ձևով ունի ձև (տես նկ. 2):

Հատկանշական հավասարման k արմատը փոխարինելով (2) համակարգով՝ եզակի մատրիցով գծային հավասարումների համասեռ համակարգ (նրա որոշիչը զրո է)։ Այս համակարգի յուրաքանչյուր ոչ զրոյական լուծում A մատրիցի սեփական վեկտորն է, որը համապատասխանում է տվյալ սեփական արժեքին k (այսինքն՝ բնորոշ հավասարման արմատը):

Օրինակ. Գտեք A մատրիցայի սեփական արժեքները և վեկտորները (տես գծապատկեր 3): Բնութագրական հավասարումը ներկայացված է Նկ. 3. Ընդարձակե՛ք որոշիչը և գտե՛ք մատրիցայի սեփական արժեքները, որոնք տրված հավասարումն են (3-k)(-1-k)-5=0, (k-3)(k+1)-5=0. , k^2-2k -8=0 Նրա արմատներն են՝ k1=4, k2=-2

ա) k1=4-ին համապատասխան սեփական վեկտորները հայտնաբերվում են (A-4kE)х=0 համակարգը լուծելով։ Այս դեպքում պահանջվում է դրա հավասարումներից միայն մեկը, քանի որ համակարգի որոշիչն ակնհայտորեն հավասար է զրոյի: Եթե ​​դնենք x=(x1, x2)^T, ապա համակարգի առաջին հավասարումը (1-4)x1+x2=0, -3x1+x2=0 է։ Եթե ​​ընդունենք, որ x1=1 (բայց ոչ զրո), ապա x2=3։ Քանի որ եզակի մատրիցով միատարր համակարգն ունի այնքան ոչ զրոյական լուծումներ, որքան ցանկալի է, ապա առաջին սեփական արժեքին համապատասխանող սեփական վեկտորների ամբողջ բազմությունը x =C1(1, 3), C1=const:

բ) Գտե՛ք k2=-2-ին համապատասխան սեփական վեկտորները։ (A+2kE)x=0 համակարգը լուծելիս նրա առաջին հավասարումն է (3+2)x1+x2=0, 5x1+x2=0, եթե դնենք x1=1, ապա x2=-5։ Համապատասխան սեփական վեկտորները x =C2(1, 3), C2=կոնստ. Տրված մատրիցայի բոլոր սեփական վեկտորների ընդհանուր բազմությունը՝ x = C1(1, 3)+ C2(1, 3):

Աղբյուրներ:

• Պիսկունով Ն.Ս. Դիֆերենցիալ և ինտեգրալ հաշվարկ: Մ., 1976, - 576 էջ.
• գտնել սեփական արժեքներ և մատրիցային վեկտորներ

Մատրիցները, որոնք տվյալների գրանցման աղյուսակային ձև են, լայնորեն կիրառվում են գծային հավասարումների համակարգերի հետ աշխատելիս։ Ընդ որում, հավասարումների թիվը որոշում է մատրիցայի տողերի թիվը, իսկ փոփոխականների թիվը՝ դրա սյունակների հերթականությունը։ Արդյունքում, գծային համակարգերի լուծումը վերածվում է մատրիցների վրա գործող գործողությունների, որոնցից մեկը մատրիցայի սեփական արժեքների հայտնաբերումն է: Նրանց հաշվարկը կատարվում է օգտագործելով բնորոշ հավասարումը: Սեփական արժեքները կարող են սահմանվել m կարգի քառակուսի մատրիցայի համար:

Հրահանգներ

Գրի՛ր տրված Ա քառակուսին: Նրա սեփական արժեքները գտնելու համար օգտագործի՛ր գծային միատարր համակարգի ոչ տրիվիալ լուծման պայմանից ստացված բնորոշ հավասարումը, որն այս դեպքում ներկայացված է քառակուսի մատրիցով: Ինչպես հետևում է Կրամերից, լուծումը գոյություն ունի միայն այն դեպքում, եթե դրա որոշիչը հավասար է զրոյի: Այսպիսով, մենք կարող ենք գրել հավասարումը | A - λE | = 0, որտեղ A-ն տրված արժեքն է, λ-ը՝ պահանջվող թվերը, E-ն նույնական մատրիցն է, որտեղ հիմնական անկյունագծով բոլոր տարրերը հավասար են մեկի, իսկ մնացածը հավասար են զրոյի։

Բազմապատկեք ցանկալի փոփոխականը λ նույնականացման մատրիցով E նույն չափի, ինչ տրված բնօրինակը A: Գործողության արդյունքը կլինի մատրիցա, որտեղ λ-ի արժեքները գտնվում են հիմնական անկյունագծով, մնացած տարրերը մնում են հավասար զրոյի: .

Անկյունագծային մատրիցներն ունեն ամենապարզ կառուցվածքը։ Հարց է առաջանում՝ հնարավո՞ր է հիմք գտնել, որում մատրիցան գծային օպերատորկունենար անկյունագծային տեսք։ Նման հիմք կա.
Մեզ տրվի R n գծային տարածություն և դրանում գործող գծային A օպերատոր; այս դեպքում օպերատոր A-ն իր մեջ վերցնում է R n-ը, այսինքն՝ A:R n → R n:

Սահմանում. Ոչ զրոյական x վեկտորը կոչվում է A օպերատորի սեփական վեկտոր, եթե A օպերատորը x-ը վերածում է համագիծ վեկտորի, այսինքն. λ թիվը կոչվում է A օպերատորի սեփական արժեք կամ սեփական արժեք, որը համապատասխանում է x սեփական վեկտորին։
Եկեք նշենք սեփական արժեքների և սեփական վեկտորների որոշ հատկություններ:
1. Սեփական վեկտորների ցանկացած գծային համակցություն Օպերատոր A-ն, որը համապատասխանում է նույն սեփական արժեքին, λ, նույն սեփական արժեքով սեփական վեկտոր է:
2. Սեփական վեկտորներ A օպերատորը զույգերով տարբեր սեփական արժեքներով λ 1 , λ 2 , ..., λ m են գծային անկախ:
3. Եթե սեփական արժեքները λ 1 =λ 2 = λ m = λ, ապա λ սեփական արժեքը համապատասխանում է ոչ ավելի, քան m գծային անկախ սեփական վեկտորներին:

Այսպիսով, եթե կան n գծային անկախ սեփական վեկտորներ , համապատասխանում են տարբեր սեփական արժեքներին λ 1, λ 2, ..., λ n, ապա դրանք գծային անկախ են, հետևաբար, դրանք կարելի է ընդունել որպես R n տարածության հիմք։ Եկեք գտնենք A գծային օպերատորի մատրիցայի ձևը նրա սեփական վեկտորների հիման վրա, որի համար մենք գործելու ենք A օպերատորի հետ հիմքի վեկտորների վրա. Հետո .
Այսպիսով, գծային A օպերատորի մատրիցը իր սեփական վեկտորների հիման վրա ունի անկյունագծային ձև, իսկ A օպերատորի սեփական արժեքները գտնվում են անկյունագծով:
Կա՞ մեկ այլ հիմք, որի դեպքում մատրիցն ունի անկյունագծային ձև: Այս հարցի պատասխանը տրվում է հետևյալ թեորեմով.

Թեորեմ. Գծային A օպերատորի մատրիցը հիմքում (i = 1..n) ունի անկյունագծային ձև, եթե և միայն այն դեպքում, եթե հիմքի բոլոր վեկտորները A օպերատորի սեփական վեկտորներն են:

Սեփական արժեքներ և սեփական վեկտորներ գտնելու կանոն

Թող տրվի վեկտոր , որտեղ x 1 , x 2 , …, x n են x վեկտորի կոորդինատները՝ հիմքի նկատմամբ իսկ x-ը գծային A օպերատորի սեփական վեկտորն է, որը համապատասխանում է λ սեփական արժեքին, այսինքն. Այս հարաբերությունը կարելի է գրել մատրիցային տեսքով

. (*)

Հավասարումը (*) կարելի է համարել x գտնելու հավասարում, և, այսինքն, մեզ հետաքրքրում են ոչ տրիվիալ լուծումները, քանի որ սեփական վեկտորը չի կարող զրո լինել։ Հայտնի է, որ գծային հավասարումների միատարր համակարգի ոչ տրիվիալ լուծումներ գոյություն ունեն, եթե և միայն այն դեպքում, եթե det(A - λE) = 0: Այսպիսով, որպեսզի λ լինի A օպերատորի սեփական արժեքը, անհրաժեշտ և բավարար է, որ det(A - λE) ) = 0.
Եթե ​​հավասարումը (*) մանրամասն գրված է կոորդինատային ձևով, մենք ստանում ենք գծային միատարր հավասարումների համակարգ.

(1)
Որտեղ - գծային օպերատորի մատրիցա:

Համակարգը (1) ունի ոչ զրոյական լուծում, եթե նրա որոշիչը D-ն հավասար է զրոյի

Մենք ստացել ենք սեփական արժեքներ գտնելու հավասարում:
Այս հավասարումը կոչվում է բնորոշ հավասարում, իսկ ձախ կողմը կոչվում է A մատրիցի բնորոշ բազմանդամը (օպերատոր): Եթե բնորոշ բազմանդամը չունի իրական արմատներ, ապա A մատրիցը չունի սեփական վեկտորներ և չի կարող վերածվել անկյունագծային ձևի:
Թող λ 1, λ 2, …, λ n լինեն բնորոշ հավասարման իրական արմատները, և դրանց մեջ կարող են լինել բազմապատիկ: Փոխարինելով այս արժեքներն իր հերթին համակարգի (1), մենք գտնում ենք սեփական վեկտորները:

Օրինակ 12. Գծային A օպերատորը գործում է R 3-ում օրենքի համաձայն, որտեղ x 1, x 2, .., x n հիմքում ընկած վեկտորի կոորդինատներն են: , , . Գտեք այս օպերատորի սեփական արժեքները և սեփական վեկտորները:
Լուծում. Մենք կառուցում ենք այս օպերատորի մատրիցը.
.
Մենք ստեղծում ենք սեփական վեկտորների կոորդինատների որոշման համակարգ.

Մենք կազմում ենք բնորոշ հավասարում և լուծում այն.

.
λ 1,2 = -1, λ 3 = 3:
Փոխարինելով λ = -1 համակարգում, մենք ունենք.
կամ
Որովհետև , ապա կան երկու կախյալ փոփոխականներ և մեկ ազատ փոփոխական։
Թող x 1-ը լինի ազատ անհայտ, ուրեմն Մենք լուծում ենք այս համակարգը ցանկացած ձևով և գտնում ենք այս համակարգի ընդհանուր լուծումը. Լուծումների հիմնարար համակարգը բաղկացած է մեկ լուծումից, քանի որ n - r = 3 - 2 = 1:
λ = -1 սեփական արժեքին համապատասխան սեփական վեկտորների բազմությունն ունի ձև՝ , որտեղ x 1-ը զրոյից տարբերվող ցանկացած թիվ է։ Եկեք այս բազմությունից ընտրենք մեկ վեկտոր, օրինակ՝ դնելով x 1 = 1: .
Նմանապես պատճառաբանելով՝ մենք գտնում ենք սեփական վեկտորը, որը համապատասխանում է սեփական արժեքին λ = 3: .
R 3 տարածության մեջ հիմքը բաղկացած է երեք գծային անկախ վեկտորներից, բայց մենք ստացանք միայն երկու գծային անկախ սեփական վեկտոր, որոնցից R 3-ում հիմքը չի կարող կազմվել։ Հետևաբար, մենք չենք կարող գծային օպերատորի A մատրիցը վերածել անկյունագծային ձևի:

Օրինակ 13. Տրվում է մատրիցա .
1. Ապացուցեք, որ վեկտորը A մատրիցի սեփական վեկտորն է: Գտեք այս սեփական վեկտորին համապատասխան սեփական արժեքը:
2. Գտե՛ք հիմք, որում A մատրիցը ունի անկյունագծային ձև:
Լուծում.
1. Եթե , ապա x-ը սեփական վեկտոր է

.
Վեկտորը (1, 8, -1) սեփական վեկտոր է: Սեփական արժեք λ = -1:
Մատրիցը ունի անկյունագծային ձև, որը բաղկացած է սեփական վեկտորներից: Նրանցից մեկը հայտնի է. Մնացածը գտնենք։
Մենք փնտրում ենք սեփական վեկտորներ համակարգից.

Բնութագրական հավասարում. ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1:
Գտնենք λ = -3 սեփական արժեքին համապատասխան սեփական վեկտորը:

Այս համակարգի մատրիցայի աստիճանը երկու է և հավասար է անհայտների թվին, ուստի այս համակարգն ունի միայն զրոյական լուծում x 1 = x 3 = 0: x 2 այստեղ կարող է լինել որևէ այլ բան, քան զրո, օրինակ, x 2 = 1. Այսպիսով, վեկտորը (0 ,1,0) λ = -3-ին համապատասխան սեփական վեկտոր է։ Եկեք ստուգենք.
.
Եթե ​​λ = 1, ապա մենք ստանում ենք համակարգը
Մատրիցայի աստիճանը երկու է: Մենք խաչում ենք վերջին հավասարումը.
Թող x 3-ը լինի անվճար անհայտ: Այնուհետև x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3:
Ենթադրելով x 3 = 1, մենք ունենք (-3,-9,1) - λ = 1 սեփական արժեքին համապատասխան սեփական վեկտոր: Ստուգեք.

.
Քանի որ սեփական արժեքները իրական են և հստակ, դրանց համապատասխան վեկտորները գծային անկախ են, ուստի դրանք կարող են հիմք ընդունել R3-ում: Այսպիսով, հիմքում , , A մատրիցը ունի ձև.
.
A:R n → R n գծային օպերատորի ոչ բոլոր մատրիցները կարող են վերածվել անկյունագծային, քանի որ որոշ գծային օպերատորների համար կարող են լինել n-ից պակաս գծային անկախ սեփական վեկտորներ: Այնուամենայնիվ, եթե մատրիցը սիմետրիկ է, ապա m բազմակիության բնորոշ հավասարման արմատը համապատասխանում է հենց m գծային անկախ վեկտորներին:

Սահմանում. Սիմետրիկ մատրիցը քառակուսի մատրից է, որում հիմնական անկյունագծի նկատմամբ սիմետրիկ տարրերը հավասար են, այսինքն, որում:
Նշումներ. 1. Սիմետրիկ մատրիցայի բոլոր սեփական արժեքները իրական են:
2. Զույգ տարբեր սեփական արժեքներին համապատասխանող սիմետրիկ մատրիցայի սեփական վեկտորները ուղղանկյուն են:
Որպես ուսումնասիրված ապարատի բազմաթիվ կիրառություններից մեկը՝ մենք դիտարկում ենք երկրորդ կարգի կորի տեսակի որոշման խնդիրը։

«Առաջին մասը սահմանում է այն դրույթները, որոնք նվազագույն անհրաժեշտ են քիմիաչափությունը հասկանալու համար, իսկ երկրորդ մասը պարունակում է փաստեր, որոնք դուք պետք է իմանաք բազմաչափ վերլուծության մեթոդները ավելի խորը հասկանալու համար: Ներկայացումը պատկերված է Excel-ի աշխատանքային գրքում արված օրինակներով: Matrix.xls, որն ուղեկցում է այս փաստաթղթին։

Օրինակների հղումները տեղադրվում են տեքստում որպես Excel օբյեկտներ: Այս օրինակները իրենց բնույթով վերացական են, դրանք ոչ մի կերպ կապված չեն անալիտիկ քիմիայի խնդիրների հետ։ Քիմիոմետրիկության մեջ մատրիցային հանրահաշվի կիրառման իրական օրինակները քննարկվում են այլ տեքստերում, որոնք ընդգրկում են մի շարք քիմիաչափական կիրառություններ:

Անալիտիկ քիմիայում կատարված չափումների մեծ մասը ուղղակի չեն, բայց անուղղակի. Սա նշանակում է, որ փորձի ժամանակ ցանկալի անալիտի C արժեքի փոխարեն (կոնցենտրացիան) ստացվում է մեկ այլ արժեք. x(ազդանշան), կապված, բայց ոչ հավասար C-ին, այսինքն. x(C) ≠ C. Որպես կանոն, կախվածության տեսակը x(C) անհայտ է, բայց, բարեբախտաբար, անալիտիկ քիմիայում չափումների մեծ մասը համամասնական է: Սա նշանակում է, որ C-ի կոնցենտրացիայի աճով աանգամ, X ազդանշանը կաճի նույն չափով, այսինքն. x(աԳ) = ա x(C). Բացի այդ, ազդանշանները նաև հավելում են, ուստի նմուշից ստացվող ազդանշանը, որում առկա են C 1 և C 2 կոնցենտրացիաներով երկու նյութեր, հավասար կլինի յուրաքանչյուր բաղադրիչի ազդանշանների գումարին, այսինքն. x(C 1 + C 2) = x(C 1)+ x(C 2): Համաչափությունն ու հավելյալությունը միասին տալիս են գծայինություն. Գծայինության սկզբունքը լուսաբանելու համար կարելի է բերել բազմաթիվ օրինակներ, սակայն բավական է նշել երկու ամենավառ օրինակները՝ քրոմատագրությունը և սպեկտրոսկոպիան։ Երկրորդ հատկանիշը, որը բնորոշ է անալիտիկ քիմիայի փորձին բազմալիքային. Ժամանակակից վերլուծական սարքավորումները միաժամանակ չափում են ազդանշանները բազմաթիվ ալիքների համար: Օրինակ, լույսի հաղորդման ինտենսիվությունը չափվում է միանգամից մի քանի ալիքի երկարության համար, այսինքն. սպեկտրը։ Ուստի փորձի ժամանակ մենք գործ ունենք բազմաթիվ ազդանշանների հետ x 1 , x 2 ,...., x n, որը բնութագրում է ուսումնասիրվող համակարգում առկա նյութերի C 1 , C 2 , ..., C m կոնցենտրացիաների բազմությունը։

Բրինձ. 1 Սպեկտրա

Այսպիսով, վերլուծական փորձը բնութագրվում է գծայինությամբ և բազմաչափությամբ: Հետևաբար, հարմար է փորձարարական տվյալները դիտարկել որպես վեկտորներ և մատրիցներ և շահարկել դրանք՝ օգտագործելով մատրիցային հանրահաշվի ապարատը։ Այս մոտեցման արդյունավետությունը ցույց է տրված օրինակով, որը ներկայացնում է երեք սպեկտրներ, որոնք վերցված են 200 ալիքի երկարությամբ 4000-ից մինչև 4796 սմ −1: Առաջինը ( x 1) և երկրորդը ( x 2) սպեկտրները ստացվել են ստանդարտ նմուշների համար, որոնցում հայտնի են A և B երկու նյութերի կոնցենտրացիաները՝ առաջին նմուշում [A] = 0,5, [B] = 0,1, իսկ երկրորդ նմուշում [A] = 0,2, [ B] = 0,6: Ինչ կարելի է ասել նոր, անհայտ նմուշի մասին, որի սպեկտրը նշված է x 3 ?

Դիտարկենք երեք փորձարարական սպեկտր x 1 , x 2 և x 3-ը որպես 200 չափման երեք վեկտոր: Օգտագործելով գծային հանրահաշիվը, կարելի է հեշտությամբ ցույց տալ դա x 3 = 0.1 x 1 +0.3 x 2, ուստի երրորդ նմուշն ակնհայտորեն պարունակում է միայն A և B նյութերը [A] = 0,5×0,1 + 0,2×0,3 = 0,11 և [B] = 0,1×0,1 + 0,6×0,3 = 0,19 կոնցենտրացիաներում:

1. Հիմնական տեղեկություններ

1.1 Մատրիցներ

Մատրիցակոչվում է թվերի ուղղանկյուն աղյուսակ, օրինակ

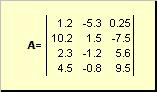
Բրինձ. 2 Մատրիցա

Մատրիցները նշվում են մեծատառ տառերով ( Ա), և դրանց տարրերը՝ համապատասխան փոքրատառերով ինդեքսներով, այսինքն. ա ij. Առաջին ինդեքսը համարակալում է տողերը, իսկ երկրորդը՝ սյունակները։ Քիմոմետիկայի մեջ ընդունված է ինդեքսի առավելագույն արժեքը նշել նույն տառով, ինչ ինդեքսը, բայց մեծատառերով։ Հետևաբար մատրիցը Ակարելի է գրել նաև որպես ( ա ij , ես = 1,..., Ի; ժ = 1,..., Ջ) Օրինակի մատրիցայի համար Ի = 4, Ջ= 3 և ա 23 = −7.5.

Զույգ թվեր ԻԵվ Ջկոչվում է մատրիցայի չափ և նշվում է որպես Ի× Ջ. Քիմիոմետրիկայի մեջ մատրիցայի օրինակ է ստացված սպեկտրների բազմությունը Ինմուշներ համար Ջալիքի երկարություններ.

1.2. Ամենապարզ գործողությունները մատրիցներով

Մատրիցները կարող են լինել բազմապատկել թվերով. Այս դեպքում յուրաքանչյուր տարր բազմապատկվում է այս թվով: Օրինակ -

Բրինձ. 3 Մատրիցը թվով բազմապատկելը

Նույն հարթության երկու մատրիցա կարող է լինել տարր առ տարր ծալելԵվ հանել. Օրինակ՝

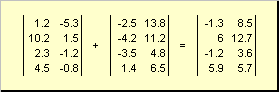
Բրինձ. 4 Մատրիցայի ավելացում

Թվով բազմապատկելու և գումարման արդյունքում ստացվում է նույն չափի մատրիցա։

Զրոյական մատրիցը զրոյից բաղկացած մատրից է: Նշանակված է Օ. Ակնհայտ է, որ Ա+Օ = Ա, Ա−Ա = Օև 0 Ա = Օ.

Մատրիցը կարող է լինել փոխադրել. Այս գործողության ընթացքում մատրիցը շրջվում է, այսինքն. տողերն ու սյունակները փոխանակվում են: Փոխադրումը նշվում է պարզ նշանով, Ա«կամ ինդեքս Ատ. Այսպիսով, եթե Ա = {ա ij , ես = 1,..., Ի; ժ = 1,...,Ջ), դա Ա t = ( ա ջի , ժ = 1,...,Ջ; i = 1,..., Ի) Օրինակ

Բրինձ. 5 Մատրիցային փոխադրում

Ակնհայտ է, որ ( Ատ) տ = Ա, (Ա+Բ) տ = Ա t+ Բտ.

1.3. Մատրիցային բազմապատկում

Մատրիցները կարող են լինել բազմապատկել, բայց միայն այն դեպքում, եթե դրանք ունենան համապատասխան չափսեր։ Թե ինչու է դա այդպես, պարզ կլինի սահմանումից: Մատրիցային արտադրանք Ա, չափս Ի× Կ, և մատրիցներ Բ, չափս Կ× Ջ, կոչվում է մատրիցա Գ, չափս Ի× Ջ, որի տարրերը թվերն են

Այսպիսով, արտադրանքի համար ԱԲանհրաժեշտ է, որ ձախ մատրիցում սյունակների քանակը Ահավասար էր աջ մատրիցայի տողերի թվին Բ. Մատրիցային արտադրանքի օրինակ -

Նկ.6 Մատրիցների արտադրյալ

Մատրիցային բազմապատկման կանոնը կարող է ձևակերպվել հետևյալ կերպ. Մատրիցային տարր գտնելու համար Գ, կանգնած խաչմերուկում ես-րդ գիծը և ժ-րդ սյունակ ( գ ij) պետք է բազմապատկել տարր առ տարր ես- առաջին մատրիցայի-րդ շարքը Ավրա ժերկրորդ մատրիցայի սյունակ Բև ավելացրեք բոլոր արդյունքները: Այսպիսով, ցույց տրված օրինակում երրորդ տողից և երկրորդ սյունակից տարրը ստացվում է որպես երրորդ շարքի տարրական արտադրյալների գումար։ Աև երկրորդ սյունակ Բ

Նկ.7 Մատրիցների արտադրյալի տարր

Մատրիցների արտադրյալը կախված է հերթականությունից, այսինքն. ԱԲ ≠ Բ.Ա., գոնե ծավալային պատճառներով։ Ասում են՝ ոչ փոխադարձ է։ Այնուամենայնիվ, մատրիցների արտադրյալը ասոցիատիվ է: Սա նշանակում է, որ ABC = (ԱԲ)Գ = Ա(Ք.ա.) Բացի այդ, այն նաև բաշխիչ է, այսինքն. Ա(Բ+Գ) = ԱԲ+A.C.. Ակնհայտ է, որ Ա.Օ. = Օ.

1.4. Քառակուսի մատրիցներ

Եթե ​​մատրիցայի սյունակների թիվը հավասար է նրա տողերի թվին ( Ի = J=N), ապա այդպիսի մատրիցը կոչվում է քառակուսի: Այս բաժնում մենք կքննարկենք միայն այդպիսի մատրիցները: Այս մատրիցներից կարելի է առանձնացնել հատուկ հատկություններով մատրիցներ։

Միայնակմատրիցա (նշված է ես,և երբեմն Ե) մատրից է, որտեղ բոլոր տարրերը հավասար են զրոյի, բացառությամբ անկյունագծերի, որոնք հավասար են 1-ի, այսինքն.

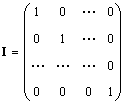
Ակնհայտորեն Ա.Ի. = Ի.Ա. = Ա.

Մատրիցը կոչվում է անկյունագծային, եթե նրա բոլոր տարրերը, բացի անկյունագծերից ( ա ii) հավասար են զրոյի: Օրինակ

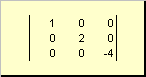
Բրինձ. 8 Անկյունագծային մատրիցա

Մատրիցա Ակոչվում է գագաթ եռանկյունաձեւ, եթե նրա բոլոր տարրերը, որոնք ընկած են անկյունագծից ներքև, հավասար են զրոյի, այսինքն. ա ij= 0, ժամը ես>ժ. Օրինակ

Բրինձ. 9 Վերին եռանկյունի մատրիցա

Ստորին եռանկյունի մատրիցը սահմանվում է նույն կերպ:

Մատրիցա Ականչեց սիմետրիկ, Եթե Ա t = Ա. Այլ կերպ ասած ա ij = ա ջի. Օրինակ

Բրինձ. 10 Սիմետրիկ մատրիցա

Մատրիցա Ականչեց ուղղանկյուն, Եթե

Ատ Ա = Ա.Ա. t = Ի.

Մատրիցը կոչվում է նորմալԵթե

1.5. Հետք և որոշիչ

Հաջորդըքառակուսի մատրիցա Ա(նշվում է Tr-ով Ա) կամ Sp( Ա)) նրա անկյունագծային տարրերի գումարն է,

Օրինակ՝

Բրինձ. 11 Մատրիցային հետք

Ակնհայտ է, որ

Sp(α Ա) = α Sp( Ա) Եվ

Sp( Ա+Բ) = Sp( Ա)+ Sp( Բ).

Կարելի է ցույց տալ, որ

Sp( Ա) = Sp( Ա t), Sp ( Ի) = Ն,

և նաև այն

Sp( ԱԲ) = Sp( Բ.Ա.).

Քառակուսի մատրիցայի մեկ այլ կարևոր բնութագիր այն է որոշիչ(նշվում է det( Ա)): Ընդհանուր դեպքում որոշիչի որոշումը բավականին դժվար է, ուստի մենք կսկսենք ամենապարզ տարբերակից՝ մատրիցով Աչափս (2×2): Հետո

(3×3) մատրիցայի համար որոշիչը հավասար կլինի

Մատրիցայի դեպքում ( Ն× Ն) որոշիչը հաշվարկվում է որպես գումար 1·2·3· ... · Ն= Ն! պայմաններ, որոնցից յուրաքանչյուրը հավասար է

Ցուցանիշներ կ 1 , կ 2 ,..., կ Նսահմանվում են որպես բոլոր հնարավոր պատվիրված փոխարկումներ rթվեր հավաքածուում (1, 2, ..., Ն) Մատրիցայի որոշիչի հաշվարկը բարդ ընթացակարգ է, որը գործնականում իրականացվում է հատուկ ծրագրերի միջոցով: Օրինակ՝

Բրինձ. 12 Մատրիցային որոշիչ

Նշենք միայն ակնհայտ հատկությունները.

դետ( Ի) = 1, det( Ա) = det( Ատ),

դետ( ԱԲ) = det( Ա)դեթ( Բ).

1.6. Վեկտորներ

Եթե ​​մատրիցը բաղկացած է միայն մեկ սյունակից ( Ջ= 1), ապա կոչվում է այդպիսի օբյեկտ վեկտոր. Ավելի ճիշտ՝ սյունակ վեկտոր։ Օրինակ

Կարելի է նաև դիտարկել, օրինակ, մեկ տողից բաղկացած մատրիցներ

Այս օբյեկտը նույնպես վեկտոր է, բայց շարքի վեկտոր. Տվյալները վերլուծելիս կարևոր է հասկանալ, թե որ վեկտորների հետ գործ ունենք՝ սյունակների կամ տողերի հետ: Այսպիսով, մեկ նմուշի համար վերցված սպեկտրը կարելի է համարել որպես տող վեկտոր: Այնուհետև բոլոր նմուշների համար որոշակի ալիքի երկարության սպեկտրային ինտենսիվությունների բազմությունը պետք է դիտարկվի որպես սյունակի վեկտոր:

Վեկտորի չափը նրա տարրերի քանակն է։

Հասկանալի է, որ ցանկացած սյունակային վեկտոր կարող է վերածվել տողային վեկտորի փոխադրման միջոցով, այսինքն.

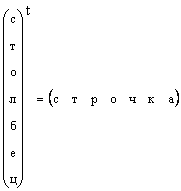
Այն դեպքերում, երբ վեկտորի ձևը հատուկ նշված չէ, այլ պարզապես ասվում է, որ վեկտոր է, ապա դրանք նշանակում են սյունակային վեկտոր: Մենք նույնպես կպահպանենք այս կանոնը. Վեկտորը նշվում է փոքրատառ, առաջ, թավ տառով: Զրոյական վեկտորը այն վեկտորն է, որի բոլոր տարրերը զրո են: Նշանակված է 0 .

1.7. Ամենապարզ գործողությունները վեկտորներով

Վեկտորները կարելի է ավելացնել և բազմապատկել թվերով այնպես, ինչպես մատրիցները։ Օրինակ՝

Բրինձ. 13 Վեկտորներով գործողություններ

Երկու վեկտոր xԵվ yկոչվում են համաչափ, եթե կա այնպիսի թիվ α, որ

1.8. Վեկտորների արտադրանք

Նույն հարթության երկու վեկտոր Նկարելի է բազմապատկել։ Թող լինի երկու վեկտոր x = (x 1 , x 2 ,...,xՆ)տ և y = (y 1 , y 2 ,...,y N) տ. Ղեկավարվելով տող առ սյունակ բազմապատկման կանոնով՝ մենք կարող ենք դրանցից կազմել երկու արտադրյալ. xտ yԵվ xyտ. Առաջին աշխատանքը

կանչեց սկալյարկամ ներքին. Դրա արդյունքը մի թիվ է: Այն նաև նշվում է ( x,y)= xտ y. Օրինակ՝

Բրինձ. 14 Ներքին (սկալար) արտադրանք

Երկրորդ կտոր

կանչեց արտաքին. Դրա արդյունքը չափերի մատրիցա է ( Ն× Ն) Օրինակ՝

Բրինձ. 15 Արտաքին աշխատանք

Վեկտորները, որոնց սկալյար արտադրյալը զրո է, կոչվում են ուղղանկյուն.

1.9. Վեկտորային նորմ

Իր հետ վեկտորի սկալյար արտադրյալը կոչվում է սկալյար քառակուսի: Այս արժեքը

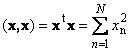
սահմանում է քառակուսի երկարությունըվեկտոր x. Երկարությունը նշելու համար (նաև կոչվում է նորմըվեկտոր) օգտագործվում է նշումը

Օրինակ՝

Բրինձ. 16 Վեկտորային նորմ

Միավոր երկարության վեկտոր (|| x|| = 1) կոչվում է նորմալացված: Ոչ զրոյական վեկտոր ( x ≠ 0 ) կարելի է նորմալացնել՝ բաժանելով երկարությամբ, այսինքն. x = ||x|| (x/||x||) = ||x|| ե. Այստեղ ե = x/||x|| - նորմալացված վեկտոր:

Վեկտորները կոչվում են օրթոնորմալ, եթե դրանք բոլորը նորմալացված են և զույգերով ուղղանկյուն:

1.10. Անկյուն վեկտորների միջև

Սկալյար արտադրյալը որոշում է և անկյունφ երկու վեկտորների միջև xԵվ y

Եթե ​​վեկտորները ուղղանկյուն են, ապա cosφ = 0 և φ = π/2, իսկ եթե դրանք համագիծ են, ապա cosφ = 1 և φ = 0:

1.11. Մատրիցայի վեկտորային ներկայացում

Յուրաքանչյուր մատրիցա Աչափը Ի× Ջկարող է ներկայացվել որպես վեկտորների մի շարք

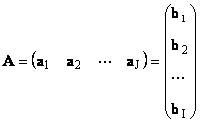
Այստեղ յուրաքանչյուր վեկտոր ա ժէ ժ-րդ սյունակը և տողի վեկտորը բ եսէ եսմատրիցայի րդ շարքը Ա

1.12. Գծային կախված վեկտորներ

Նույն չափի վեկտորներ ( Ն) կարելի է ավելացնել և բազմապատկել թվով, ինչպես մատրիցները։ Արդյունքը կլինի նույն հարթության վեկտորը: Թող լինեն նույն հարթության մի քանի վեկտորներ x 1 , x 2 ,...,x K և նույնքան թվեր α α 1 , α 2 ,...,α Կ. Վեկտոր

y= α 1 x 1 + α 2 x 2 +...+ α Կ x Կ

կանչեց գծային համադրությունվեկտորներ x կ .

Եթե ​​կան այդպիսի ոչ զրոյական α թվեր կ ≠ 0, կ = 1,..., Կ, Ինչ y = 0 , ապա վեկտորների նման հավաքածու x կկանչեց գծային կախված. Հակառակ դեպքում, ասում են, որ վեկտորները գծային անկախ են: Օրինակ՝ վեկտորները x 1 = (2, 2)տ և x 2 = (−1, −1) t գծային կախված են, քանի որ x 1 +2x 2 = 0

1.13. Մատրիցային աստիճան

Դիտարկենք մի շարք Կվեկտորներ x 1 , x 2 ,...,x Կչափերը Ն. Վեկտորների այս համակարգի աստիճանը գծային անկախ վեկտորների առավելագույն քանակն է: Օրինակ հավաքածուի մեջ

կան միայն երկու գծային անկախ վեկտորներ, օրինակ x 1 և x 2, ուստի նրա վարկանիշը 2 է:

Ակնհայտ է, որ եթե մի շարքում ավելի շատ վեկտորներ կան, քան դրանց չափերը ( Կ>Ն), ապա դրանք անպայմանորեն գծային կախված են։

Մատրիցային աստիճան(նշվում է աստիճանով) Ա)) այն վեկտորների համակարգի աստիճանն է, որից այն բաղկացած է։ Չնայած ցանկացած մատրիցա կարող է ներկայացվել երկու ձևով (սյունակ կամ տող վեկտոր), դա չի ազդում դասակարգման արժեքի վրա, քանի որ

1.14. Հակադարձ մատրիցա

Քառակուսի մատրիցա Ակոչվում է ոչ այլասերված, եթե ունի եզակի հակադարձմատրիցա Ա-1 պայմաններով որոշված

Ա.Ա. −1 = Ա −1 Ա = Ի.

Հակադարձ մատրիցը գոյություն չունի բոլոր մատրիցների համար: Ոչ այլասերվելու համար անհրաժեշտ և բավարար պայման է

դետ( Ա) ≠ 0 կամ աստիճան ( Ա) = Ն.

Matrix inversion-ը բարդ ընթացակարգ է, որի համար կան հատուկ ծրագրեր։ Օրինակ՝

Բրինձ. 17 Մատրիցային ինվերսիա

Ներկայացնենք ամենապարզ դեպքի բանաձևերը՝ 2×2 մատրիցա

Եթե ​​մատրիցներ ԱԵվ Բոչ այլասերված են, ուրեմն

(ԱԲ) −1 = Բ −1 Ա −1 .

1.15. Կեղծ հակադարձ մատրիցա

Եթե ​​մատրիցա Աեզակի է, իսկ հակադարձ մատրիցը գոյություն չունի, ապա որոշ դեպքերում կարող եք օգտագործել կեղծ հակադարձմատրիցա, որը սահմանվում է որպես այդպիսի մատրիցա Ա+ դա

Ա.Ա. + Ա = Ա.

Կեղծ հակադարձ մատրիցը միակը չէ, և դրա ձևը կախված է կառուցման մեթոդից: Օրինակ, ուղղանկյուն մատրիցայի համար կարող եք օգտագործել Moore-Penrose մեթոդը:

Եթե ​​սյունակների թիվը տողերի քանակից քիչ է, ապա

Ա + =(Ատ Ա) −1 Ատ

Օրինակ՝

Բրինձ. 17ա մատրիցայի կեղծ ինվերսիա

Եթե ​​սյունակների թիվը տողերի քանակից մեծ է, ապա

Ա + =Ատ ( Ա.Ա.տ) −1

1.16. Վեկտորի բազմապատկում մատրիցով

Վեկտոր xկարելի է բազմապատկել մատրիցով Ահարմար չափս. Այս դեպքում սյունակի վեկտորը բազմապատկվում է աջ կողմում Կացին, իսկ վեկտորային տողը ձախ կողմում է xտ Ա. Եթե ​​վեկտորի չափը Ջև մատրիցայի չափը Ի× Ջապա արդյունքը կլինի չափման վեկտոր Ի. Օրինակ՝

Բրինձ. 18 Վեկտորի բազմապատկում մատրիցով

Եթե ​​մատրիցա Ա- քառակուսի ( Ի× Ի), ապա վեկտորը y = Կացինունի նույն չափը, ինչ x. Ակնհայտ է, որ

Ա(α 1 x 1 + α 2 x 2) = α 1 Կացին 1 + α 2 Կացին 2 .

Ուստի մատրիցները կարելի է համարել որպես վեկտորների գծային փոխակերպումներ։ Մասնավորապես Իքս = x, Եզ = 0 .

2. Լրացուցիչ տեղեկություններ

2.1. Գծային հավասարումների համակարգեր

Թող Ա- մատրիցայի չափը Ի× Ջ, Ա բ- հարթության վեկտոր Ջ. Դիտարկենք հավասարումը

Կացին = բ

վեկտորի համեմատ x, չափսեր Ի. Ըստ էության, դա համակարգ է Իհետ գծային հավասարումներ Ջանհայտ x 1 ,...,x Ջ. Լուծումը գոյություն ունի, եթե և միայն այն դեպքում, եթե

կոչում ( Ա) = կոչում ( Բ) = Ռ,

Որտեղ Բչափերի ընդլայնված մատրիցա է Ի×( J+1), որը բաղկացած է մատրիցից Ա, լրացված սյունակով բ, Բ = (Ա բ) Հակառակ դեպքում, հավասարումները անհամապատասխան են:

Եթե Ռ = Ի = Ջ, ապա լուծումը եզակի է

x = Ա −1 բ.

Եթե Ռ < Ի, ապա կան բազմաթիվ տարբեր լուծումներ, որոնք կարող են արտահայտվել գծային համակցության միջոցով Ջ−Ռվեկտորներ. Միատարր հավասարումների համակարգ Կացին = 0 քառակուսի մատրիցով Ա (Ն× Ն) ունի ոչ տրիվիալ լուծում ( x ≠ 0 ) եթե և միայն եթե det( Ա) = 0. Եթե Ռ= կոչում ( Ա)<Ն, ապա կան Ն−Ռգծային անկախ լուծումներ.

2.2. Երկգծային և քառակուսի ձևեր

Եթե Աքառակուսի մատրից է, և xԵվ y- համապատասխան չափման վեկտորը, ապա ձևի սկալյար արտադրյալը xտ Այկանչեց երկգծայինմատրիցով սահմանված ձևը Ա. ժամը x = yարտահայտություն xտ Կացինկանչեց քառակուսիձևը.

2.3. Դրական որոշակի մատրիցներ

Քառակուսի մատրիցա Ականչեց դրական որոշակի, եթե որևէ ոչ զրոյական վեկտորի համար x ≠ 0 ,

xտ Կացին > 0.

Նմանապես սահմանված է բացասական (xտ Կացին < 0), ոչ բացասական (xտ Կացին≥ 0) և բացասական (xտ Կացին≤ 0) որոշակի մատրիցներ.

2.4. Չոլեսկու տարրալուծում

Եթե ​​սիմետրիկ մատրիցը Ադրական որոշակի է, ապա կա եզակի եռանկյուն մատրիցա Uդրական տարրերով, որոնց համար

Ա = Uտ U.

Օրինակ՝

Բրինձ. 19 Չոլեսկու տարրալուծում

2.5. Բևեռային տարրալուծում

Թող Աչափումների ոչ եզակի քառակուսի մատրից է Ն× Ն. Այնուհետեւ կա եզակի բևեռայինկատարումը

Ա = Ս.Ռ.

Որտեղ Սոչ բացասական սիմետրիկ մատրից է, և Ռուղղանկյուն մատրիցա է: Մատրիցներ ՍԵվ Ռկարելի է հստակորեն սահմանել.

Ս 2 = Ա.Ա.տ կամ Ս = (Ա.Ա.տ) ½ և Ռ = Ս −1 Ա = (Ա.Ա.տ) −½ Ա.

Օրինակ՝

Բրինձ. 20 Բևեռային տարրալուծում

Եթե ​​մատրիցա Ադեգեներատ է, ապա տարրալուծումը եզակի չէ, մասնավորապես. Սդեռ մենակ, բայց Ռգուցե շատ. Բևեռային տարրալուծումը ներկայացնում է մատրիցը Աորպես սեղմման/ընդլայնման համակցություն Սև շրջվել Ռ.

2.6. Սեփական վեկտորներ և սեփական արժեքներ

Թող Աքառակուսի մատրիցա է: Վեկտոր vկանչեց սեփական վեկտորմատրիցներ Ա, Եթե

Ավ = λ v,

որտեղ կոչվում է λ թիվը սեփական արժեքմատրիցներ Ա. Այսպիսով, փոխակերպումը, որը կատարում է մատրիցը Ավեկտորի վերևում v, հանգում է պարզ ձգման կամ սեղմման λ գործակցով։ Սեփական վեկտորը որոշվում է մինչև բազմապատկումը α ≠ 0 հաստատունով, այսինքն. Եթե vսեփական վեկտոր է, ապա α v- նաև սեփական վեկտոր:

2.7. Սեփական արժեքներ

Մատրիցայում Ա, չափս ( Ն× Ն) չի կարող լինել ավելի քան Նսեփական արժեքներ. Նրանք բավարարում են բնորոշ հավասարում

դետ( Ա − λ Ի) = 0,

որը հանրահաշվական հավասարում է Ն-րդ կարգը. Մասնավորապես, 2×2 մատրիցայի համար բնորոշ հավասարումն ունի ձև

Օրինակ՝

Բրինձ. 21 սեփական արժեքներ

Սեփական արժեքների բազմություն λ 1 ,..., λ Նմատրիցներ Ականչեց սպեկտրը Ա.

Սպեկտրը տարբեր հատկություններ ունի. Մասնավորապես

դետ( Ա) = λ 1 ×...×λ Ն,Sp( Ա) = λ 1 +...+λ Ն.

Կամայական մատրիցայի սեփական արժեքները կարող են լինել բարդ թվեր, բայց եթե մատրիցը սիմետրիկ է ( Ա t = Ա), ապա դրա սեփական արժեքները իրական են:

2.8. Սեփական վեկտորներ

Մատրիցայում Ա, չափս ( Ն× Ն) չի կարող լինել ավելի քան Նսեփական վեկտորներ, որոնցից յուրաքանչյուրը համապատասխանում է իր սեփական արժեքին: Որոշել սեփական վեկտորը v nանհրաժեշտ է լուծել միատարր հավասարումների համակարգ

(Ա − λ n Ի)v n = 0 .

Այն ունի ոչ տրիվիալ լուծում, քանի որ det( Ա -λ n Ի) = 0.

Օրինակ՝

Բրինձ. 22 սեփական վեկտորներ

Սիմետրիկ մատրիցայի սեփական վեկտորները ուղղանկյուն են: