www.sait võimaldab teil leida. Sait teostab arvutuse. Mõne sekundi pärast annab server õige lahenduse. Maatriksi iseloomulik võrrand on algebraline avaldis, mis leitakse determinandi arvutamise reeglit kasutades maatriksid maatriksid, samas kui põhidiagonaalis on diagonaalelementide ja muutuja väärtustes erinevusi. Arvutamisel maatriksi tunnusvõrrand võrgus, iga element maatriksid korrutatakse vastavate muude elementidega maatriksid. Otsige režiimis võrgus võimalik ainult ruudu jaoks maatriksid. Operatsiooni leidmine maatriksi tunnusvõrrand võrgus taandub elementide korrutise algebralise summa arvutamiseks maatriksid determinandi leidmise tulemusena maatriksid, ainult kindlaksmääramise eesmärgil maatriksi tunnusvõrrand võrgus. Sellel operatsioonil on teoorias eriline koht maatriksid, võimaldab juurte abil leida omaväärtusi ja vektoreid. Ülesanne leida maatriksi tunnusvõrrand võrgus koosneb korrutavatest elementidest maatriksid millele järgneb nende toodete summeerimine teatud reegli järgi. www.sait leiab maatriksi iseloomulik võrrand antud dimensioon režiimis võrgus. Arvutamine maatriksi tunnusvõrrand võrgus selle dimensiooni arvestades on see numbriliste või sümboolsete koefitsientidega polünoomi leidmine, mis leitakse vastavalt determinandi arvutamise reeglile maatriksid- vastavate elementide korrutiste summana maatriksid, ainult kindlaksmääramise eesmärgil maatriksi tunnusvõrrand võrgus. Polünoomi leidmine ruutsuuruse muutuja suhtes maatriksid, määratlusena maatriksi iseloomulik võrrand, teoreetiliselt levinud maatriksid. Polünoomi juurte tähendus maatriksi tunnusvõrrand võrgus kasutatakse omavektorite ja omaväärtuste määramiseks maatriksid. Pealegi, kui determinant maatriksid tahe võrdne nulliga, See maatriksi karakteristlik võrrand erinevalt vastupidisest on endiselt olemas maatriksid. Selleks, et arvutada maatriksi iseloomulik võrrand või leida mitu korraga maatriksite tunnusvõrrandid, peate kulutama palju aega ja vaeva, samas kui meie server leiab mõne sekundiga võrgumaatriksi tunnusvõrrand. Sel juhul vastus leidmisele maatriksi tunnusvõrrand võrgus on õige ja piisava täpsusega, isegi kui numbrid leidmisel maatriksi tunnusvõrrand võrgus saab olema irratsionaalne. Veebilehel www.sait märkide sisestamine on elementides lubatud maatriksid, see tähendab võrgumaatriksi tunnusvõrrand saab arvutamisel esitada üldisel sümboolsel kujul maatriksi iseloomulik võrrand võrgus. Saadud vastust on kasulik kontrollida leidmisülesande lahendamisel maatriksi tunnusvõrrand võrgus saidi kasutades www.sait. Polünoomi arvutamise toimingu tegemisel - maatriksi karakteristlik võrrand, peate selle probleemi lahendamisel olema ettevaatlik ja äärmiselt keskendunud. Meie sait omakorda aitab teil kontrollida oma otsust sellel teemal maatriksi tunnusvõrrand võrgus. Kui teil pole aega lahendatud probleemide pikaks kontrollimiseks, siis www.sait on kindlasti mugav tööriist otsimisel ja arvutamisel maatriksi tunnusvõrrand võrgus.

Juhised

Arvu k nimetatakse maatriksi A omaväärtuseks (arvuks), kui on olemas vektor x, mille korral Ax=kx. (1) Sel juhul nimetatakse vektorit x maatriksi A omavektoriks, mis vastab arvule k Ruumis R^n (vt joonis 1) on maatriksil A kujund nagu joonisel.

On vaja püstitada ülesanne leida maatriksi A vektorid. Olgu omavektor x antud koordinaatidega. Maatriksi kujul kirjutatakse see veerumaatriksina, mis mugavuse huvides tuleks esitada transponeeritud reana. X=(x1,x2,…,xn)^T Põhineb (1), Ax-khx=0 või Ax-kEx=0, kus E on identsusmaatriks (ühed põhidiagonaalil, kõik muud elemendid on nullid). ). Siis (A-kE)x=0. (2)

Lineaarsete homogeensete algebraliste võrrandite avaldisel (2) on nullist erinev lahend (omavektor). Seetõttu on süsteemi (2) põhideterminant võrdne nulliga, st |A-kE|=0. (3) Omaväärtuse k viimast võrdsust nimetatakse maatriksi A karakteristikuks ja laiendatud kujul on sellel kuju (vt joonis 2).

Asendades tunnusvõrrandi juure k süsteemiks (2), homogeenseks lineaarvõrrandisüsteemiks singulaarmaatriksiga (selle determinant on null). Selle süsteemi iga nullist erinev lahend on maatriksi A omavektor, mis vastab antud omaväärtusele k (st karakteristiku võrrandi juur).

Näide. Leidke maatriksi A omaväärtused ja vektorid (vt joonis 3). Iseloomulik võrrand on esitatud joonisel fig. 3. Laiendage determinanti ja leidke maatriksi omaväärtused, milleks on antud võrrand (3-k)(-1-k)-5=0, (k-3)(k+1)-5=0 , k^2-2k -8=0 Selle juured on k1=4, k2=-2

a) K1=4-le vastavad omavektorid leitakse süsteemi (A-4kE)х=0 lahendamisel. Sel juhul on vaja ainult ühte selle võrrandit, kuna süsteemi determinant on ilmselgelt võrdne nulliga. Kui panna x=(x1, x2)^T, siis on süsteemi esimene võrrand (1-4)x1+x2=0, -3x1+x2=0. Kui eeldame, et x1=1 (kuid mitte null), siis x2=3. Kuna singulaarmaatriksiga homogeensel süsteemil on nii palju nullist erinevaid lahendeid kui soovitakse, siis kogu esimesele omaväärtusele vastav omavektorite hulk x =C1(1, 3), C1=const.

b) Leia omavektorid, mis vastavad k2=-2-le. Süsteemi (A+2kE)x=0 lahendamisel on selle esimene võrrand (3+2)x1+x2=0, 5x1+x2=0 Kui paneme x1=1, siis x2=-5. Vastavad omavektorid x =C2(1, 3), C2=konst. Antud maatriksi kõigi omavektorite koguhulk: x = C1(1, 3)+ C2(1, 3).

Allikad:

• Piskunov N.S. Diferentsiaal- ja integraalarvutus. M., 1976, - 576 lk.
• leida omaväärtusi ja maatriksvektoreid

Lineaarvõrrandisüsteemidega töötamisel kasutatakse laialdaselt maatrikseid, mis on andmete salvestamise tabelivorm. Veelgi enam, võrrandite arv määrab maatriksi ridade arvu ja muutujate arv selle veergude järjekorra. Selle tulemusena taandatakse lineaarsete süsteemide lahendamine maatriksitega tehtavateks toiminguteks, millest üks on maatriksi omaväärtuste leidmine. Nende arvutamine toimub iseloomuliku võrrandi abil. Omaväärtusi saab määrata ruutmaatriksi jaoks, mille suurus on m.

Juhised

Kirjutage üles antud ruut A. Selle omaväärtuste leidmiseks kasutage lineaarse homogeense süsteemi mittetriviaalse lahenduse tingimusest tulenevat karakteristlikku võrrandit, mida antud juhul kujutab ruutmaatriks. Nagu Cramerist järeldub, on lahendus olemas ainult siis, kui selle determinant on võrdne nulliga. Seega saame kirjutada võrrandi | A - λE | = 0, kus A on antud väärtus, λ on nõutavad arvud, E on identsusmaatriks, milles kõik põhidiagonaali elemendid on võrdsed ühega ja ülejäänud on võrdsed nulliga.

Korrutage soovitud muutuja λ identiteedimaatriksiga E, mis on sama mõõtmega kui antud algne A. Tehe tulemuseks on maatriks, kus λ väärtused paiknevad piki põhidiagonaali, ülejäänud elemendid jäävad nulliks .

Diagonaalmaatriksitel on kõige lihtsam struktuur. Tekib küsimus, kas on võimalik leida alust, milles maatriks lineaarne operaator oleks diagonaalse välimusega. Selline alus on olemas.
Olgu meile antud lineaarruum R n ja selles tegutsev lineaaroperaator A; sel juhul võtab operaator A R n enda sisse, st A:R n → R n .

Definitsioon. Nullist erinevat vektorit x nimetatakse operaatori A omavektoriks, kui operaator A teisendab x kollineaarseks vektoriks, st. Arvu λ nimetatakse operaatori A omaväärtuseks või omaväärtuseks, mis vastab omavektorile x.
Märgime mõned omaväärtuste ja omavektorite omadused.
1. Omavektorite mis tahes lineaarne kombinatsioon operaator A, mis vastab samale omaväärtusele λ, on sama omaväärtusega omavektor.
2. Omavektorid operaator A paaride kaupa erinevate omaväärtustega λ 1 , λ 2 , …, λ m on lineaarselt sõltumatud.
3. Kui omaväärtused λ 1 =λ 2 = λ m = λ, siis omaväärtus λ vastab mitte rohkem kui m lineaarselt sõltumatule omavektorile.

Seega, kui on n lineaarselt sõltumatut omavektorit , mis vastavad erinevatele omaväärtustele λ 1, λ 2, ..., λ n, siis on nad lineaarselt sõltumatud, seega võib neid võtta ruumi R n aluseks. Leiame selle omavektorite alusel lineaaroperaatori A maatriksi kuju, mille puhul tegutseme operaatoriga A baasvektorite alusel: Siis .
Seega on lineaarse operaatori A maatriksil oma omavektorite alusel diagonaalkuju ja operaatori A omaväärtused on piki diagonaali.
Kas on veel mõni alus, mille puhul maatriksil on diagonaalne vorm? Sellele küsimusele annab vastuse järgmine teoreem.

Teoreem. Lineaaroperaatori A maatriksil aluses (i = 1..n) on diagonaalkuju siis ja ainult siis, kui kõik aluse vektorid on operaatori A omavektorid.

Omaväärtuste ja omavektorite leidmise reegel

Olgu vektor antud , kus x 1 , x 2 , …, x n on vektori x koordinaadid baasi suhtes ja x on lineaaroperaatori A omavektor, mis vastab omaväärtusele λ, st. Selle seose saab kirjutada maatriksi kujul

. (*)

Võrrandit (*) võib pidada võrrandiks x leidmiseks ja see tähendab, et meid huvitavad mittetriviaalsed lahendid, kuna omavektor ei saa olla null. On teada, et homogeense lineaarvõrrandisüsteemi mittetriviaalsed lahendid eksisteerivad siis ja ainult siis, kui det(A - λE) = 0. Seega, et λ oleks operaatori A omaväärtus, on vajalik ja piisav, et det(A - λE) ) = 0.
Kui võrrand (*) on üksikasjalikult kirjutatud koordinaatide kujul, saame lineaarsete homogeensete võrrandite süsteemi:

(1)
Kus - lineaarne operaatormaatriks.

Süsteemil (1) on nullist erinev lahendus, kui selle determinant D on võrdne nulliga

Saime omaväärtuste leidmiseks võrrandi.
Seda võrrandit nimetatakse karakteristikvõrrandiks ja selle vasakut poolt maatriksi (operaatori) A iseloomulikuks polünoomiks. Kui karakteristikul polünoomil pole reaaljuuri, siis maatriksil A ei ole omavektoreid ja seda ei saa taandada diagonaalkujule.
Olgu λ 1, λ 2, …, λ n karakteristikavõrrandi reaaljuured ja nende hulgas võib olla kordi. Asendades need väärtused omakorda süsteemiga (1), leiame omavektorid.

Näide 12. Lineaaroperaator A toimib R 3-s vastavalt seadusele, kus x 1, x 2, .., x n on baasis oleva vektori koordinaadid , , . Leidke selle operaatori omaväärtused ja omavektorid.
Lahendus. Koostame selle operaatori maatriksi:
.
Loome omavektorite koordinaatide määramise süsteemi:

Koostame iseloomuliku võrrandi ja lahendame selle:

.
λ 1,2 = -1, λ 3 = 3.
Asendades süsteemi λ = -1, saame:
või
Sest , siis on kaks sõltuvat muutujat ja üks vaba muutuja.
Olgu siis x 1 vaba tundmatu Me lahendame selle süsteemi mis tahes viisil ja leiame selle süsteemi üldlahenduse: Lahenduste põhisüsteem koosneb ühest lahendist, kuna n - r = 3 - 2 = 1.
Omaväärtusele λ = -1 vastav omavektorite hulk on kujul: , kus x 1 on mis tahes arv, mis ei ole null. Valime sellest hulgast ühe vektori, näiteks paneme x 1 = 1: .
Sarnaselt arutledes leiame omaväärtusele λ = 3 vastava omavektori: .
Ruumis R 3 koosneb alus kolmest lineaarselt sõltumatust vektorist, kuid saime ainult kaks lineaarselt sõltumatut omavektorit, millest R 3 baasi ei saa koostada. Järelikult ei saa me lineaaroperaatori maatriksit A ​​taandada diagonaalkujule.

Näide 13. Antud maatriks .
1. Tõesta, et vektor on maatriksi A omavektor. Leia sellele omavektorile vastav omaväärtus.
2. Leia alus, milles maatriksil A on diagonaalkuju.
Lahendus.
1. Kui , siis x on omavektor

.
Vektor (1, 8, -1) on omavektor. Omaväärtus λ = -1.
Maatriksil on omavektoritest koosnevas baasis diagonaalkuju. Üks neist on kuulus. Leiame ülejäänud.
Otsime süsteemist omavektoreid:

Iseloomulik võrrand: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2–1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Leiame omaväärtusele λ = -3 vastav omavektor:

Selle süsteemi maatriksi auaste on kaks ja võrdne tundmatute arvuga, seega on sellel süsteemil ainult nulllahendus x 1 = x 3 = 0. x 2 võib siin olla midagi muud kui null, näiteks x 2 = 1. Seega on vektor (0 ,1,0) omavektor, mis vastab väärtusele λ = -3. Kontrollime:
.
Kui λ = 1, siis saame süsteemi
Maatriksi auaste on kaks. Viimase võrrandi kriipsutame maha.
Olgu x 3 vaba tundmatu. Siis x 1 = -3x 3, 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3, x 2 = -9x 3.
Eeldusel, et x 3 = 1, on meil (-3,-9,1) - omaväärtusele λ = 1 vastav omavektor. Kontrollige:

.
Kuna omaväärtused on reaalsed ja erinevad, on neile vastavad vektorid lineaarselt sõltumatud, nii et neid saab võtta aluseks R 3 . Seega aluses , , maatriksil A on vorm:
.
Mitte iga lineaarse operaatori A:R n → R n maatriksit ei saa taandada diagonaalkujule, kuna mõne lineaaroperaatori puhul võib olla vähem kui n lineaarset sõltumatut omavektorit. Kui aga maatriks on sümmeetriline, vastab kordsuse m iseloomuliku võrrandi juur täpselt m lineaarselt sõltumatule vektorile.

Definitsioon. Sümmeetriline maatriks on ruutmaatriks, milles põhidiagonaali suhtes sümmeetrilised elemendid on võrdsed, see tähendab, milles .
Märkmed. 1. Kõik sümmeetrilise maatriksi omaväärtused on reaalsed.
2. Paarikaupa erinevatele omaväärtustele vastava sümmeetrilise maatriksi omavektorid on ortogonaalsed.
Üheks paljudest uuritud aparaadi rakendustest käsitleme teist järku kõvera tüübi määramise probleemi.

"Esimeses osas on välja toodud sätted, mis on minimaalselt vajalikud kemomeetria mõistmiseks ja teises osas faktid, mida on vaja teada mitmemõõtmelise analüüsi meetodite sügavamaks mõistmiseks. Esitlust illustreerivad Exceli töövihikus tehtud näited Matrix.xls, mis on selle dokumendiga kaasas.

Lingid näidetele paigutatakse teksti Exceli objektidena. Need näited on oma olemuselt abstraktsed, need ei ole kuidagi seotud analüütilise keemia probleemidega. Elulisi näiteid maatriksalgebra kasutamisest kemomeetrias on käsitletud teistes tekstides, mis hõlmavad mitmesuguseid kemomeetrilisi rakendusi.

Enamik analüütilises keemias tehtud mõõtmisi ei ole otsesed, vaid kaudne. See tähendab, et katses saadakse soovitud analüüdi C väärtuse (kontsentratsiooni) asemel teine ​​väärtus x(signaal), seotud, kuid mitte võrdne C-ga, st. x(C) ≠ C. Reeglina sõltuvuse tüüp x(C) on teadmata, kuid õnneks on analüütilises keemias enamik mõõtmisi proportsionaalsed. See tähendab, et C kontsentratsiooni suurenemisega in a korda, suureneb signaal X sama palju, st. x(a C) = a x(C). Lisaks on signaalid ka aditiivsed, nii et proovist, milles on kaks ainet kontsentratsiooniga C 1 ja C 2, saadav signaal on võrdne iga komponendi signaalide summaga, s.o. x(C1 + C2) = x(C1)+ x(C 2). Proportsionaalsus ja liitlikkus koos annavad lineaarsus. Lineaarsuse printsiibi illustreerimiseks võib tuua palju näiteid, kuid piisab, kui mainida kahte kõige markantsemat näidet – kromatograafiat ja spektroskoopiat. Teine omadus, mis on omane analüütilise keemia katsele, on mitme kanaliga. Kaasaegsed analüütilised seadmed mõõdavad samaaegselt paljude kanalite signaale. Näiteks mõõdetakse valguse läbilaskvuse intensiivsust mitme lainepikkuse puhul korraga, s.t. spekter. Seetõttu tegeleme katses paljude signaalidega x 1 , x 2 ,...., x n, mis iseloomustab uuritavas süsteemis esinevate ainete kontsentratsioonide kogumit C 1 , C 2 , ..., C m.

Riis. 1 spekter

Niisiis iseloomustab analüütilist katset lineaarsus ja mitmemõõtmelisus. Seetõttu on mugav käsitleda eksperimentaalseid andmeid vektorite ja maatriksitena ning nendega manipuleerida maatriksalgebra aparaadi abil. Selle lähenemisviisi viljakust illustreerib näide, mis kujutab endast kolme spektrit, mis on võetud 200 lainepikkusel vahemikus 4000 kuni 4796 cm -1. Esiteks ( x 1) ja teine ​​( x 2) spektrid saadi standardproovidele, milles on teada kahe aine A ja B kontsentratsioonid: esimeses proovis [A] = 0,5, [B] = 0,1 ja teises proovis [A] = 0,2, [ B] = 0,6. Mida saab öelda uue, tundmatu valimi kohta, mille spekter on näidatud x 3 ?

Vaatleme kolme eksperimentaalset spektrit x 1 , x 2 ja x 3 kui kolm vektorit mõõtmega 200. Lineaaralgebra abil saab seda lihtsalt näidata x 3 = 0.1 x 1 +0.3 x 2, seega sisaldab kolmas proov ilmselgelt ainult aineid A ja B kontsentratsioonides [A] = 0,5 × 0,1 + 0,2 × 0,3 = 0,11 ja [B] = 0,1 × 0,1 + 0,6 × 0,3 = 0,19.

1. Põhiteave

1.1 Maatriksid

Maatriks nimetatakse näiteks ristkülikukujuliseks arvutabeliks

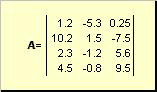
Riis. 2 Maatriks

Maatriksid on tähistatud suurte paksude tähtedega ( A), ja nende elemendid - vastavate väiketähtedega koos indeksitega, s.o. a ij. Esimene indeks nummerdab read ja teine ​​- veerud. Kemomeetrias on tavaks tähistada indeksi maksimaalset väärtust sama tähega kui indeks ise, kuid suurtähtedega. Seetõttu maatriks A võib kirjutada ka kui ( a ij , i = 1,..., I; j = 1,..., J). Näidismaatriksi jaoks I = 4, J= 3 ja a 23 = −7.5.

Numbripaar I Ja J nimetatakse maatriksi dimensiooniks ja tähistatakse kui I× J. Maatriksi näide kemomeetrias on spektrite kogum, mis on saadud jaoks I proovid jaoks J lainepikkused.

1.2. Lihtsamad tehted maatriksitega

Maatriksid võivad olla arvudega korrutada. Sel juhul korrutatakse iga element selle arvuga. Näiteks -

Riis. 3 Maatriksi korrutamine arvuga

Kaks sama dimensiooniga maatriksit võivad olla elemendi kaupa voltida Ja lahutada. Näiteks

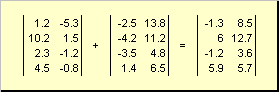
Riis. 4 Maatriksi liitmine

Arvuga korrutamise ja liitmise tulemusena saadakse sama mõõtmega maatriks.

Nullmaatriks on maatriks, mis koosneb nullidest. See on määratud O. See on ilmne A+O = A, A−A = O ja 0 A = O.

Maatriks võib olla üle võtta. Selle toimingu ajal pööratakse maatriksit, st. read ja veerud vahetatakse. Ülevõtmist tähistatakse algarvuga, A" või indeks A t. Seega, kui A = {a ij , i = 1,..., I; j = 1,...,J), See A t = ( a ji , j = 1,...,J; i = 1,..., I). Näiteks

Riis. 5 Maatriksi ülevõtmine

On ilmne, et ( A t) t = A, (A+B) t = A t+ B t.

1.3. Maatrikskorrutis

Maatriksid võivad olla korrutada, kuid ainult siis, kui neil on sobivad mõõtmed. Miks see nii on, selgub määratlusest. Matrix toode A, mõõde I× K, ja maatriksid B, mõõde K× J, nimetatakse maatriksiks C, mõõde I× J, mille elemendid on numbrid

Seega toote jaoks AB on vajalik, et veergude arv vasakpoolses maatriksis A oli võrdne ridade arvuga parempoolses maatriksis B. Maatrikstoote näide -

Joonis 6 Maatriksite korrutis

Maatrikskorrutamise reegli saab sõnastada järgmiselt. Maatriksielemendi leidmiseks C, seisab ristmikul i-th rida ja j veerg ( c ij) tuleb korrutada elemendi kaupa i- esimese maatriksi rida A sisse j teise maatriksi veerus B ja liita kõik tulemused kokku. Nii et näidatud näites saadakse element kolmandast reast ja teisest veerust kolmanda rea ​​elemendipõhiste korrutiste summana A ja teine ​​veerg B

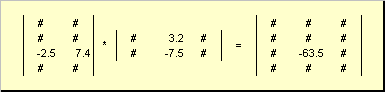
Joon.7 Maatriksite korrutise element

Maatriksite korrutis oleneb järjekorrast, s.o. AB ≠ B.A., vähemalt mõõtmete tõttu. Nad ütlevad, et see on mittekommutatiivne. Maatriksite korrutis on aga assotsiatiivne. See tähendab, et ABC = (AB)C = A(B.C.). Lisaks on see ka distributiivne, st. A(B+C) = AB+A.C.. See on ilmne A.O. = O.

1.4. Ruutmaatriksid

Kui maatriksi veergude arv on võrdne selle ridade arvuga ( I = J=N), siis nimetatakse sellist maatriksit ruuduks. Selles jaotises käsitleme ainult selliseid maatrikseid. Nende maatriksite hulgas võib eristada eriomadustega maatrikseid.

Vallaline maatriks (tähistatud mina, ja mõnikord E) on maatriks, milles kõik elemendid on võrdsed nulliga, välja arvatud diagonaalid, mis on võrdsed 1-ga, s.o.

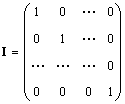
Ilmselgelt A.I. = I.A. = A.

Maatriksit nimetatakse diagonaal, kui kõik selle elemendid, välja arvatud diagonaalsed ( a ii) on võrdsed nulliga. Näiteks

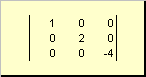
Riis. 8 Diagonaalmaatriks

Maatriks A nimetatakse tippu kolmnurkne, kui kõik selle diagonaalist allpool asuvad elemendid on võrdsed nulliga, s.o. a ij= 0, at i>j. Näiteks

Riis. 9 Ülemine kolmnurkmaatriks

Alumine kolmnurkne maatriks on määratletud sarnaselt.

Maatriks A helistas sümmeetriline, Kui A t = A. Teisisõnu a ij = a ji. Näiteks

Riis. 10 Sümmeetriline maatriks

Maatriks A helistas ortogonaalne, Kui

A t A = A.A. t = I.

Maatriksit nimetatakse normaalne Kui

1.5. Jälg ja määraja

Edasi ruutmaatriks A(tähistatud Tr( A) või Sp( A)) on selle diagonaalsete elementide summa,

Näiteks

Riis. 11 Maatriksi jälg

See on ilmne

Sp(α A) = α Sp( A) Ja

Sp( A+B) = Sp( A)+ Sp( B).

Seda saab näidata

Sp( A) = Sp( A t), Sp( I) = N,

ja ka seda

Sp( AB) = Sp( B.A.).

Ruutmaatriksi teine ​​oluline omadus on see determinant(tähistatud det( A)). Determinandi määramine üldjuhul on üsna keeruline, seega alustame kõige lihtsamast võimalusest - maatriksist A mõõt (2 × 2). Siis

(3 × 3) maatriksi puhul on determinant võrdne

Maatriksi puhul ( N× N) determinant arvutatakse summana 1·2·3· ... · N= N! terminid, millest igaüks on võrdne

Indeksid k 1 , k 2 ,..., k N on määratletud kui kõik võimalikud järjestatud permutatsioonid r numbrid komplektis (1, 2, ..., N). Maatriksi determinandi arvutamine on keeruline protseduur, mis praktikas viiakse läbi spetsiaalsete programmide abil. Näiteks

Riis. 12 Maatriksdeterminant

Märgime ainult ilmseid omadusi:

det( I) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vektorid

Kui maatriks koosneb ainult ühest veerust ( J= 1), siis nimetatakse sellist objekti vektor. Täpsemalt veeruvektor. Näiteks

Arvestada võib ka näiteks ühest reast koosnevaid maatrikseid

See objekt on samuti vektor, kuid rea vektor. Andmete analüüsimisel on oluline mõista, milliste vektoritega on tegemist – veergude või ridadega. Seega võib ühe proovi jaoks võetud spektrit pidada reavektoriks. Seejärel tuleks kõigi proovide teatud lainepikkustel spektriintensiivsuse kogumit käsitleda kolonnivektorina.

Vektori mõõde on selle elementide arv.

On selge, et iga veeruvektorit saab muuta reavektoriks transpositsiooniga, s.t.

Juhtudel, kui vektori kuju ei ole konkreetselt määratletud, vaid lihtsalt öeldakse, et see on vektor, tähendab see veeru vektorit. Peame ka sellest reeglist kinni. Vektorit tähistatakse väikese, püstise, paksu tähega. Nullvektor on vektor, mille kõik elemendid on nullid. See on määratud 0 .

1.7. Lihtsamad toimingud vektoritega

Vektoreid saab liita ja arvudega korrutada samamoodi nagu maatrikseid. Näiteks

Riis. 13 Tehted vektoritega

Kaks vektorit x Ja y kutsutakse kolineaarne, kui on olemas selline arv α, et

1.8. Vektorite produktid

Kaks sama mõõtmega vektorit N saab korrutada. Olgu kaks vektorit x = (x 1 , x 2 ,...,x N)t ja y = (y 1 , y 2 ,...,y N) t. Järgides ridade kaupa korrutamise reeglit, saame neist koostada kaks korrutist: x t y Ja xy t. Esimene töö

helistas skalaar või sisemine. Selle tulemus on arv. Seda tähistatakse ka ( x,y)= x t y. Näiteks

Riis. 14 Sisemine (skalaarne) korrutis

Teine tükk

helistas välised. Selle tulemuseks on mõõtmete maatriks ( N× N). Näiteks

Riis. 15 Välistööd

Nimetatakse vektoreid, mille skalaarkorrutis on null ortogonaalne.

1.9. Vektori norm

Vektori skalaarkorrutist iseendaga nimetatakse skalaarruuduks. See väärtus

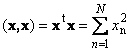
määrab ruudu pikkus vektor x. Pikkuse näitamiseks (nimetatakse ka norm vektor) kasutatakse tähistust

Näiteks

Riis. 16 Vektornorm

Ühiku pikkuse vektor (|| x|| = 1) nimetatakse normaliseeritud. nullist erinev vektor ( x ≠ 0 ) saab normaliseerida, jagades selle pikkusega, s.t. x = ||x|| (x/||x||) = ||x|| e. Siin e = x/||x|| - normaliseeritud vektor.

Vektoreid nimetatakse ortonormaalseteks, kui need kõik on normaliseeritud ja paarikaupa ortogonaalsed.

1.10. Nurk vektorite vahel

Skalaarkorrutis määrab ja nurgasφ kahe vektori vahel x Ja y

Kui vektorid on ortogonaalsed, siis cosφ = 0 ja φ = π/2 ning kui need on kolineaarsed, siis cosφ = 1 ja φ = 0.

1.11. Maatriksi vektorkujutus

Iga maatriks A suurus I× J saab esitada vektorite hulgana

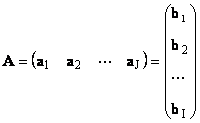
Siin on iga vektor a j on j veerg ja rea ​​vektor b i on i maatriksi rida A

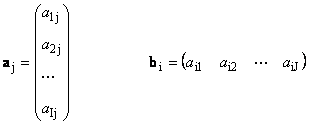
1.12. Lineaarselt sõltuvad vektorid

Sama mõõtmega vektorid ( N) saab liita ja korrutada arvuga, nagu maatriksitegi. Tulemuseks on sama mõõtmega vektor. Olgu mitu sama mõõtmega vektorit x 1 , x 2 ,...,x K ja sama arv numbreid α α 1 , α 2 ,..., α K. Vektor

y= α 1 x 1 + α 2 x 2 +...+ α K x K

helistas lineaarne kombinatsioon vektorid x k .

Kui on selliseid nullist erinevaid arve α k ≠ 0, k = 1,..., K, Mida y = 0 , siis selline vektorite hulk x k helistas lineaarselt sõltuv. Vastasel juhul öeldakse, et vektorid on lineaarselt sõltumatud. Näiteks vektorid x 1 = (2, 2)t ja x 2 = (−1, −1) t on lineaarselt sõltuvad, sest x 1 +2x 2 = 0

1.13. Maatriksi auaste

Kaaluge komplekti K vektorid x 1 , x 2 ,...,x K mõõtmed N. Selle vektorite süsteemi järjestus on lineaarselt sõltumatute vektorite maksimaalne arv. Näiteks komplektis

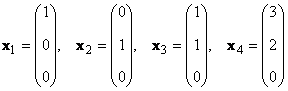
näiteks on ainult kaks lineaarselt sõltumatut vektorit x 1 ja x 2, seega on selle auaste 2.

Ilmselgelt, kui hulga vektoreid on rohkem kui nende mõõde ( K>N), siis on need tingimata lineaarselt sõltuvad.

Maatriksi auaste(tähistatud auastmega( A)) on selle vektorite süsteemi aste, millest see koosneb. Kuigi mis tahes maatriksit saab esitada kahel viisil (veeru- või reavektorid), ei mõjuta see järjestuse väärtust, sest

1.14. Pöördmaatriks

Ruutmaatriks A nimetatakse mitte-degeneratiivseks, kui sellel on kordumatu vastupidine maatriks A-1, määratakse tingimustega

A.A. −1 = A −1 A = I.

Pöördmaatriksit ei eksisteeri kõigi maatriksite jaoks. Mittemandastumise vajalik ja piisav tingimus on

det( A) ≠ 0 või auaste( A) = N.

Maatriksi inversioon on keeruline protseduur, mille jaoks on olemas spetsiaalsed programmid. Näiteks

Riis. 17 Maatriksi inversioon

Toome välja kõige lihtsama juhtumi – 2×2 maatriksi – valemid

Kui maatriksid A Ja B on siis mitte-mandunud

(AB) −1 = B −1 A −1 .

1.15. Pseudoinversne maatriks

Kui maatriks A on ainsuses ja pöördmaatriksit ei eksisteeri, siis mõnel juhul võite kasutada pseudoinversne maatriks, mis on määratletud sellise maatriksina A+ see

A.A. + A = A.

Pseudoinversne maatriks pole ainus ja selle vorm sõltub ehitusmeetodist. Näiteks ristkülikukujulise maatriksi jaoks võite kasutada Moore-Penrose'i meetodit.

Kui veergude arv on väiksem kui ridade arv, siis

A + =(A t A) −1 A t

Näiteks

Riis. 17a Maatriksi pseudoinversioon

Kui veergude arv on suurem kui ridade arv, siis

A + =A t ( A.A. t) −1

1.16. Vektori korrutamine maatriksiga

Vektor x saab korrutada maatriksiga A sobiv suurus. Sel juhul korrutatakse veeruvektor paremal Ax, ja vektori rida on vasakul x t A. Kui vektori mõõde J ja maatriksi mõõde I× J siis on tulemuseks mõõtmevektor I. Näiteks

Riis. 18 Vektori korrutamine maatriksiga

Kui maatriks A- ruut ( I× I), siis vektor y = Ax on sama mõõtmega kui x. See on ilmne

A(α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Seetõttu võib maatrikseid pidada vektorite lineaarseteks teisendusteks. Eelkõige Ix = x, Ox = 0 .

2. Lisainfo

2.1. Lineaarvõrrandisüsteemid

Lase A- maatriksi suurus I× J, A b- mõõtmete vektor J. Mõelge võrrandile

Ax = b

vektori suhtes x, mõõtmed I. Põhimõtteliselt on see süsteem I lineaarvõrrandid J teadmata x 1 ,...,x J. Lahendus on olemas siis ja ainult siis

rank( A) = auaste( B) = R,

Kus B on laiendatud mõõtmete maatriks I×( J+1), mis koosneb maatriksist A, mida täiendab veerg b, B = (A b). Vastasel juhul on võrrandid vastuolulised.

Kui R = I = J, siis on lahendus ainulaadne

x = A −1 b.

Kui R < I, siis on palju erinevaid lahendusi, mida saab väljendada läbi lineaarse kombinatsiooni J−R vektorid. Homogeensete võrrandite süsteem Ax = 0 ruutmaatriksiga A (N× N) omab mittetriviaalset lahendust ( x ≠ 0 ) siis ja ainult siis, kui det( A) = 0. Kui R= rank( A)<N, siis neid on N−R lineaarselt sõltumatud lahendused.

2.2. Bilineaarsed ja ruutvormid

Kui A on ruutmaatriks ja x Ja y- vastava mõõtme vektor, seejärel vormi skalaarkorrutis x t Ah helistas bilineaarne maatriksiga määratletud vorm A. Kell x = y väljendus x t Ax helistas ruutkeskne vormi.

2.3. Positiivsed kindlad maatriksid

Ruutmaatriks A helistas positiivne kindel, kui mis tahes nullist erineva vektori korral x ≠ 0 ,

x t Ax > 0.

Sarnaselt määratletud negatiivne (x t Ax < 0), mittenegatiivne (x t Ax≥ 0) ja negatiivne (x t Ax≤ 0) teatud maatriksid.

2.4. Cholesky lagunemine

Kui sümmeetriline maatriks A on positiivne kindel, siis on olemas ainulaadne kolmnurkmaatriks U positiivsete elementidega, mille jaoks

A = U t U.

Näiteks

Riis. 19 Cholesky lagunemine

2.5. Polaarne lagunemine

Lase A on mõõtmete mitteainsuse ruutmaatriks N× N. Siis on unikaalne polaarne esitus

A = S.R.

Kus S on mittenegatiivne sümmeetriline maatriks ja R on ortogonaalne maatriks. Maatriksid S Ja R saab selgelt määratleda:

S 2 = A.A. t või S = (A.A. t) ½ ja R = S −1 A = (A.A. t) −½ A.

Näiteks

Riis. 20 Polaarne lagunemine

Kui maatriks A on degenereerunud, siis lagunemine pole ainulaadne - nimelt: S ikka üksi, aga R võibolla palju. Polaarne lagunemine esindab maatriksit A kompressiooni/pikenduste kombinatsioonina S ja pöörake R.

2.6. Omavektorid ja omaväärtused

Lase A on ruutmaatriks. Vektor v helistas omavektor maatriksid A, Kui

Av = λ v,

kus kutsutakse arvu λ omaväärtus maatriksid A. Seega teisendus, mille maatriks teostab A vektori kohal v, taandub lihtsale venitamisele või kokkusurumisele koefitsiendiga λ. Omavektor määratakse kuni korrutamiseni konstandiga α ≠ 0, st. Kui v on omavektor, siis α v- ka omavektor.

2.7. Omaväärtused

Maatriksi juures A, mõõde ( N× N) ei saa olla suurem kui N omaväärtused. Nad rahuldavad iseloomulik võrrand

det( A − λ I) = 0,

mis on algebraline võrrand N- järjekorras. Täpsemalt, 2 × 2 maatriksi puhul on iseloomuliku võrrandi vorm

Näiteks

Riis. 21 Omaväärtused

Omaväärtuste komplekt λ 1 ,..., λ N maatriksid A helistas spekter A.

Spektril on erinevad omadused. Eelkõige

det( A) = λ 1 ×... × λ N,Sp( A) = λ 1 +...+λ N.

Suvalise maatriksi omaväärtused võivad olla kompleksarvud, kuid kui maatriks on sümmeetriline ( A t = A), siis on selle omaväärtused reaalsed.

2.8. Omavektorid

Maatriksi juures A, mõõde ( N× N) ei saa olla suurem kui N omavektorid, millest igaüks vastab oma omaväärtusele. Omavektori määramiseks v n vaja lahendada homogeensete võrrandite süsteem

(A − λ n I)v n = 0 .

Sellel on mittetriviaalne lahendus, kuna det( A -λ n I) = 0.

Näiteks

Riis. 22 omavektorit

Sümmeetrilise maatriksi omavektorid on ortogonaalsed.