HOMOGEENSTE LINEAARVÕRRANDITE SÜSTEEM

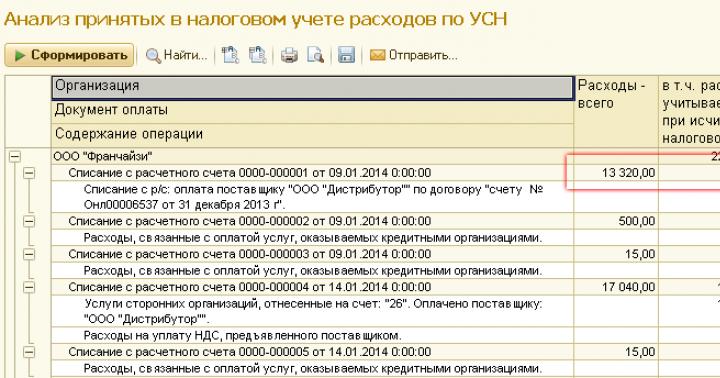
Homogeensete lineaarvõrrandite süsteem on vormi süsteem

Selge on see, et antud juhul , sest nende determinantide ühe veeru kõik elemendid on võrdsed nulliga.

Kuna tundmatud leitakse valemite järgi , siis juhul, kui Δ ≠ 0, on süsteemil unikaalne nulllahendus x = y = z= 0. Paljude ülesannete puhul on aga huvitav küsimus, kas homogeensel süsteemil on nullist erinevaid lahendeid.

Teoreem. Selleks, et lineaarsete homogeensete võrrandite süsteemil oleks nullist erinev lahendus, on vajalik ja piisav, et Δ ≠ 0.

Seega, kui determinant Δ ≠ 0, siis on süsteemil ainulaadne lahendus. Kui Δ ≠ 0, siis on lineaarsete homogeensete võrrandite süsteemil lõpmatu arv lahendeid.

Näited.

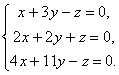
Maatriksi omavektorid ja omaväärtused

Olgu antud ruutmaatriks , X– mingi maatriks-veerg, mille kõrgus langeb kokku maatriksi järjekorraga A. .

Paljude ülesannete puhul peame arvestama võrrandiga X

kus λ on teatud arv. On selge, et mis tahes λ korral on sellel võrrandil nulllahendus.

Nimetatakse arvu λ, mille jaoks sellel võrrandil on nullist erinevad lahendid omaväärtus maatriksid A, A X sellise λ jaoks nimetatakse omavektor maatriksid A.

Leiame maatriksi omavektori A. Sest E∙X = X, siis saab maatriksvõrrandi ümber kirjutada kujul või . Laiendatud kujul saab selle võrrandi ümber kirjutada lineaarsete võrrandite süsteemiks. Tõesti .

Ja seetõttu

Niisiis, oleme saanud koordinaatide määramiseks homogeensete lineaarvõrrandite süsteemi x 1, x 2, x 3 vektor X. Et süsteemis oleks nullist erineva lahendusi, on vajalik ja piisav, et süsteemi determinant oleks võrdne nulliga, s.t.

See on λ 3. astme võrrand. Seda nimetatakse iseloomulik võrrand maatriksid A ja seda kasutatakse λ omaväärtuste määramiseks.

Iga omaväärtus λ vastab omavektorile X, mille koordinaadid määratakse süsteemist vastava väärtusega λ.

Näited.

VEKTORALGEBRA. VEKTORI MÕISTE

Erinevate füüsikaharude uurimisel on suurused, mis määratakse täielikult kindlaks nende arvväärtuste täpsustamisega, näiteks pikkus, pindala, mass, temperatuur jne. Selliseid suurusi nimetatakse skalaarideks. Kuid lisaks neile on olemas ka suurused, mille määramiseks on lisaks arvväärtusele vaja teada ka nende suunda ruumis, näiteks kehale mõjuvat jõudu, keha kiirust ja kiirendust. keha, kui see ruumis liigub, pinge magnetväli antud ruumipunktis jne. Selliseid suurusi nimetatakse vektorsuurusteks.

Tutvustame ranget määratlust.

Suunatud segment Nimetame lõigu, mille otste suhtes on teada, milline neist on esimene ja milline teine.

Vektor nimetatakse teatud pikkusega suunatud segmendiks, st. See on teatud pikkusega segment, milles üks seda piiravatest punktidest võetakse alguseks ja teine ​​​​lõpuks. Kui A- vektori algus, B on selle lõpp, siis tähistatakse vektorit sümboliga, lisaks tähistatakse vektorit sageli ühe tähega. Joonisel on vektorit tähistatud segmendiga ja selle suunda noolega.

Moodul või pikkus Vektoriks nimetatakse seda määratleva suunatud segmendi pikkust. Tähistatakse || või ||.

Samuti lisame vektoritena nn nullvektori, mille algus ja lõpp langevad kokku. See on määratud. Nullvektoril ei ole kindlat suunda ja selle moodul on võrdne nulliga ||=0.

Vektoreid nimetatakse kollineaarne, kui need asuvad samal joonel või paralleelsetel joontel. Veelgi enam, kui vektorid ja on samas suunas, kirjutame , vastupidine.

Nimetatakse vektoreid, mis asuvad sama tasapinnaga paralleelsetel sirgel koplanaarne.

Neid kahte vektorit nimetatakse võrdne, kui need on kollineaarsed, on samasuunalised ja võrdse pikkusega. Sel juhul kirjutavad nad.

Vektorite võrdsuse definitsioonist järeldub, et vektorit saab transportida paralleelselt iseendaga, asetades selle alguse mis tahes ruumipunkti.

Näiteks.

LINEAARSED TEHTUD VEKTORIDELE

1. Vektori korrutamine arvuga.

   Vektori ja arvu λ korrutis on uus vektor, nii et:

   Vektori ja arvu λ korrutist tähistatakse .

   

   Näiteks on vektor, mis on suunatud vektoriga samas suunas ja mille pikkus on poole vektori pikkusest.

   Kasutusele võetud toimingul on järgmine omadused:

2. Vektori lisamine.

   Olgu ja kaks suvalist vektorit. Võtame meelevaldse punkti O ja konstrueerida vektor. Pärast seda punktist A jätame vektori kõrvale. Nimetatakse vektor, mis ühendab esimese vektori alguse teise lõpuga summa nendest vektoritest ja on tähistatud .

   

   Vektorliitmise formuleeritud definitsiooni nimetatakse rööpküliku reegel, kuna sama vektorite summa võib saada järgmiselt. Lükkame punktist edasi O vektorid ja . Koostame nendele vektoritele rööpküliku OABC. Kuna vektorid, siis vektor, mis on tipust tõmmatud rööpküliku diagonaal O, on ilmselt vektorite summa.

   

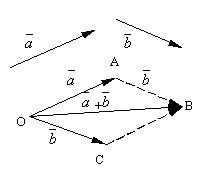
   Seda on lihtne kontrollida vektori liitmise omadused.

3. Vektori erinevus.

   Nimetatakse antud vektoriga kollineaarset vektorit, mis on võrdne pikkusega ja vastupidise suunaga vastupidine vektor vektori jaoks ja seda tähistatakse . Vastandvektorit võib pidada vektori arvuga λ = –1 korrutamise tulemuseks: .

"Esimeses osas on välja toodud sätted, mis on minimaalselt vajalikud kemomeetria mõistmiseks ja teises osas faktid, mida on vaja teada mitmemõõtmelise analüüsi meetodite sügavamaks mõistmiseks. Esitlust illustreerivad Exceli töövihikus tehtud näited Matrix.xls, mis on selle dokumendiga kaasas.

Lingid näidetele paigutatakse teksti Exceli objektidena. Need näited on oma olemuselt abstraktsed, need ei ole kuidagi seotud analüütilise keemia probleemidega. Elulisi näiteid maatriksalgebra kasutamisest kemomeetrias on käsitletud teistes tekstides, mis hõlmavad mitmesuguseid kemomeetrilisi rakendusi.

Enamik analüütilises keemias tehtud mõõtmisi ei ole otsesed, vaid kaudne. See tähendab, et katses saadakse soovitud analüüdi C väärtuse (kontsentratsiooni) asemel teine ​​väärtus x(signaal), seotud, kuid mitte võrdne C-ga, st. x(C) ≠ C. Reeglina sõltuvuse tüüp x(C) on teadmata, kuid õnneks on analüütilises keemias enamik mõõtmisi proportsionaalsed. See tähendab, et C kontsentratsiooni suurenemisega in a korda, suureneb signaal X sama palju, st. x(a C) = a x(C). Lisaks on signaalid ka aditiivsed, nii et proovist, milles on kaks ainet kontsentratsiooniga C 1 ja C 2, saadav signaal on võrdne iga komponendi signaalide summaga, s.o. x(C1 + C2) = x(C1)+ x(C 2). Proportsionaalsus ja liitlikkus koos annavad lineaarsus. Lineaarsuse printsiibi illustreerimiseks võib tuua palju näiteid, kuid piisab, kui mainida kahte kõige markantsemat näidet – kromatograafiat ja spektroskoopiat. Teine omadus, mis on omane analüütilise keemia katsele, on mitme kanaliga. Kaasaegsed analüütilised seadmed mõõdavad samaaegselt paljude kanalite signaale. Näiteks mõõdetakse valguse läbilaskvuse intensiivsust mitme lainepikkuse puhul korraga, s.t. spekter. Seetõttu tegeleme katses paljude signaalidega x 1 , x 2 ,...., x n, mis iseloomustab uuritavas süsteemis esinevate ainete kontsentratsioonide kogumit C 1 , C 2 , ..., C m.

Riis. 1 spekter

Niisiis iseloomustab analüütilist katset lineaarsus ja mitmemõõtmelisus. Seetõttu on mugav käsitleda eksperimentaalseid andmeid vektorite ja maatriksitena ning nendega manipuleerida maatriksalgebra aparaadi abil. Selle lähenemisviisi viljakust illustreerib näide, mis kujutab endast kolme spektrit, mis on võetud 200 lainepikkusel vahemikus 4000 kuni 4796 cm -1. Esiteks ( x 1) ja teine ​​( x 2) spektrid saadi standardproovidele, milles on teada kahe aine A ja B kontsentratsioonid: esimeses proovis [A] = 0,5, [B] = 0,1 ja teises proovis [A] = 0,2, [ B] = 0,6. Mida saab öelda uue, tundmatu valimi kohta, mille spekter on näidatud x 3 ?

Vaatleme kolme eksperimentaalset spektrit x 1 , x 2 ja x 3 kui kolm vektorit dimensiooniga 200. Lineaaralgebra abil saab seda lihtsalt näidata x 3 = 0.1 x 1 +0.3 x 2, seega sisaldab kolmas proov ilmselgelt ainult aineid A ja B kontsentratsioonides [A] = 0,5 × 0,1 + 0,2 × 0,3 = 0,11 ja [B] = 0,1 × 0,1 + 0,6 × 0,3 = 0,19.

1. Põhiteave

1.1 Maatriksid

Maatriks nimetatakse näiteks ristkülikukujuliseks arvutabeliks

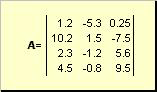
Riis. 2 Maatriks

Maatriksid on tähistatud suurte paksude tähtedega ( A), ja nende elemendid - vastavate väiketähtedega koos indeksitega, s.t. a ij. Esimene indeks nummerdab read ja teine ​​- veerud. Kemomeetrias on tavaks tähistada indeksi maksimaalset väärtust sama tähega kui indeks ise, kuid suurtähtedega. Seetõttu maatriks A võib kirjutada ka kui ( a ij , i = 1,..., I; j = 1,..., J). Näidismaatriksi jaoks I = 4, J= 3 ja a 23 = −7.5.

Numbripaar I Ja J nimetatakse maatriksi dimensiooniks ja tähistatakse kui I× J. Maatriksi näide kemomeetrias on spektrite kogum, mis on saadud jaoks I proovid jaoks J lainepikkused.

1.2. Lihtsamad tehted maatriksitega

Maatriksid võivad olla arvudega korrutada. Sel juhul korrutatakse iga element selle arvuga. Näiteks -

Riis. 3 Maatriksi korrutamine arvuga

Kaks sama dimensiooniga maatriksit võivad olla elemendi kaupa voltida Ja lahutada. Näiteks

Riis. 4 Maatriksi liitmine

Arvuga korrutamise ja liitmise tulemusena saadakse sama mõõtmega maatriks.

Nullmaatriks on maatriks, mis koosneb nullidest. See on määratud O. See on ilmne A+O = A, A−A = O ja 0 A = O.

Maatriks võib olla üle võtta. Selle toimingu ajal pööratakse maatriksit, st. read ja veerud vahetatakse. Ülevõtmist tähistatakse algarvuga, A" või indeks A t. Seega, kui A = {a ij , i = 1,..., I; j = 1,...,J), See A t = ( a ji , j = 1,...,J; i = 1,..., I). Näiteks

Riis. 5 Maatriksi ülevõtmine

On ilmne, et ( A t) t = A, (A+B) t = A t+ B t.

1.3. Maatrikskorrutis

Maatriksid võivad olla korrutada, kuid ainult siis, kui neil on sobivad mõõtmed. Miks see nii on, selgub määratlusest. Matrix toode A, mõõde I× K, ja maatriksid B, mõõde K× J, nimetatakse maatriksiks C, mõõde I× J, mille elemendid on arvud

Seega toote jaoks AB on vajalik, et veergude arv vasakpoolses maatriksis A oli võrdne ridade arvuga parempoolses maatriksis B. Maatrikstoote näide -

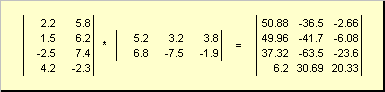
Joonis 6 Maatriksite korrutis

Maatrikskorrutamise reegli saab sõnastada järgmiselt. Maatriksielemendi leidmiseks C, seisab ristmikul i-th rida ja j veerg ( c ij) tuleb korrutada elemendi kaupa i- esimese maatriksi rida A sisse j teise maatriksi veerus B ja liita kõik tulemused kokku. Nii et näidatud näites saadakse element kolmandast reast ja teisest veerust kolmanda rea ​​elemendipõhiste korrutiste summana A ja teine ​​veerg B

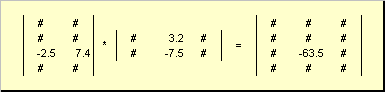
Joon.7 Maatriksite korrutise element

Maatriksite korrutis oleneb järjekorrast, s.o. AB ≠ B.A., vähemalt mõõtmete tõttu. Nad ütlevad, et see on mittekommutatiivne. Maatriksite korrutis on aga assotsiatiivne. See tähendab, et ABC = (AB)C = A(B.C.). Lisaks on see ka distributiivne, st. A(B+C) = AB+A.C.. See on ilmne A.O. = O.

1.4. Ruutmaatriksid

Kui maatriksi veergude arv on võrdne selle ridade arvuga ( I = J=N), siis nimetatakse sellist maatriksit ruuduks. Selles jaotises käsitleme ainult selliseid maatrikseid. Nende maatriksite hulgas võib eristada eriomadustega maatrikseid.

Vallaline maatriks (tähistatud mina, ja mõnikord E) on maatriks, milles kõik elemendid on võrdsed nulliga, välja arvatud diagonaalid, mis on võrdsed 1-ga, s.o.

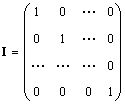
Ilmselgelt A.I. = I.A. = A.

Maatriksit nimetatakse diagonaal, kui kõik selle elemendid, välja arvatud diagonaalsed ( a ii) on võrdsed nulliga. Näiteks

Riis. 8 Diagonaalmaatriks

Maatriks A nimetatakse tippu kolmnurkne, kui kõik selle diagonaalist allpool asuvad elemendid on võrdsed nulliga, s.o. a ij= 0, at i>j. Näiteks

Riis. 9 Ülemine kolmnurkmaatriks

Alumine kolmnurkne maatriks on määratletud sarnaselt.

Maatriks A helistas sümmeetriline, Kui A t = A. Teisisõnu a ij = a ji. Näiteks

Riis. 10 Sümmeetriline maatriks

Maatriks A helistas ortogonaalne, Kui

A t A = A.A. t = I.

Maatriksit nimetatakse normaalne Kui

1.5. Jälg ja määraja

Edasi ruutmaatriks A(tähistatud Tr( A) või Sp( A)) on selle diagonaalsete elementide summa,

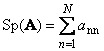
Näiteks

Riis. 11 Maatriksi jälg

See on ilmne

Sp(α A) = α Sp( A) Ja

Sp( A+B) = Sp( A)+ Sp( B).

Seda saab näidata

Sp( A) = Sp( A t), Sp( I) = N,

ja ka seda

Sp( AB) = Sp( B.A.).

Ruutmaatriksi teine ​​oluline omadus on see determinant(tähistatud det( A)). Determinandi määramine üldjuhul on üsna keeruline, seega alustame kõige lihtsamast võimalusest - maatriksist A mõõt (2 × 2). Siis

Maatriksi (3 × 3) korral on determinant võrdne

Maatriksi puhul ( N× N) determinant arvutatakse summana 1·2·3· ... · N= N! terminid, millest igaüks on võrdne

Indeksid k 1 , k 2 ,..., k N on määratletud kui kõik võimalikud järjestatud permutatsioonid r numbrid komplektis (1, 2, ..., N). Maatriksi determinandi arvutamine on keeruline protseduur, mis praktikas viiakse läbi spetsiaalsete programmide abil. Näiteks

Riis. 12 Maatriksdeterminant

Märgime ainult ilmseid omadusi:

det( I) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vektorid

Kui maatriks koosneb ainult ühest veerust ( J= 1), siis nimetatakse sellist objekti vektor. Täpsemalt veeruvektor. Näiteks

Arvestada võib ka näiteks ühest reast koosnevaid maatrikseid

See objekt on samuti vektor, kuid rea vektor. Andmete analüüsimisel on oluline mõista, milliste vektoritega on tegemist – veergude või ridadega. Seega võib ühe proovi jaoks võetud spektrit pidada reavektoriks. Seejärel tuleks kõigi proovide teatud lainepikkustel spektriintensiivsuse kogumit käsitleda kolonnivektorina.

Vektori mõõde on selle elementide arv.

On selge, et iga veeruvektorit saab muuta reavektoriks transpositsiooniga, s.t.

Juhtudel, kui vektori kuju ei ole konkreetselt välja toodud, vaid lihtsalt öeldakse, et see on vektor, tähendab see veeruvektorit. Peame ka sellest reeglist kinni. Vektorit tähistatakse väikese, edasisuunatud, paksu tähega. Nullvektor on vektor, mille kõik elemendid on nullid. See on määratud 0 .

1.7. Lihtsamad toimingud vektoritega

Vektoreid saab liita ja arvudega korrutada samamoodi nagu maatrikseid. Näiteks

Riis. 13 Tehted vektoritega

Kaks vektorit x Ja y kutsutakse kolineaarne, kui on olemas selline arv α, et

1.8. Vektorite produktid

Kaks sama mõõtmega vektorit N saab korrutada. Olgu kaks vektorit x = (x 1 , x 2 ,...,x N)t ja y = (y 1 , y 2 ,...,y N) t. Järgides ridade kaupa korrutamise reeglit, saame neist koostada kaks korrutist: x t y Ja xy t. Esimene töö

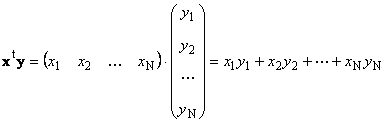
helistas skalaar või sisemine. Selle tulemus on arv. Seda tähistatakse ka ( x,y)= x t y. Näiteks

Riis. 14 Sisemine (skalaarne) korrutis

Teine tükk

helistas välised. Selle tulemuseks on mõõtmete maatriks ( N× N). Näiteks

Riis. 15 Välistööd

Nimetatakse vektoreid, mille skalaarkorrutis on null ortogonaalne.

1.9. Vektori norm

Vektori skalaarkorrutist iseendaga nimetatakse skalaarruuduks. See väärtus

määrab ruudu pikkus vektor x. Pikkuse näitamiseks (nimetatakse ka norm vektor) kasutatakse tähistust

Näiteks

Riis. 16 Vektornorm

Ühiku pikkuse vektor (|| x|| = 1) nimetatakse normaliseeritud. nullist erinev vektor ( x ≠ 0 ) saab normaliseerida, jagades selle pikkusega, s.t. x = ||x|| (x/||x||) = ||x|| e. Siin e = x/||x|| - normaliseeritud vektor.

Vektoreid nimetatakse ortonormaalseteks, kui need kõik on normaliseeritud ja paarikaupa ortogonaalsed.

1.10. Nurk vektorite vahel

Skalaarkorrutis määrab ja nurgasφ kahe vektori vahel x Ja y

Kui vektorid on ortogonaalsed, siis cosφ = 0 ja φ = π/2 ning kui need on kolineaarsed, siis cosφ = 1 ja φ = 0.

1.11. Maatriksi vektorkujutus

Iga maatriks A suurus I× J saab esitada vektorite hulgana

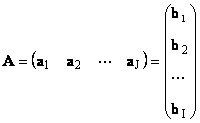
Siin on iga vektor a j on j veerg ja reavektor b i on i maatriksi rida A

1.12. Lineaarselt sõltuvad vektorid

Sama mõõtmega vektorid ( N) saab liita ja korrutada arvuga, nagu maatriksitegi. Tulemuseks on sama mõõtmega vektor. Olgu mitu sama mõõtmega vektorit x 1 , x 2 ,...,x K ja sama arv numbreid α α 1 , α 2 ,..., α K. Vektor

y= α 1 x 1 + α 2 x 2 +...+ α K x K

helistas lineaarne kombinatsioon vektorid x k .

Kui on selliseid nullist erinevaid arve α k ≠ 0, k = 1,..., K, Mida y = 0 , siis selline vektorite hulk x k helistas lineaarselt sõltuv. Vastasel juhul öeldakse, et vektorid on lineaarselt sõltumatud. Näiteks vektorid x 1 = (2, 2)t ja x 2 = (−1, −1) t on lineaarselt sõltuvad, sest x 1 +2x 2 = 0

1.13. Maatriksi auaste

Kaaluge komplekti K vektorid x 1 , x 2 ,...,x K mõõtmed N. Selle vektorite süsteemi järjestus on lineaarselt sõltumatute vektorite maksimaalne arv. Näiteks komplektis

näiteks on ainult kaks lineaarselt sõltumatut vektorit x 1 ja x 2, seega on selle auaste 2.

Ilmselgelt, kui hulga vektoreid on rohkem kui nende mõõde ( K>N), siis on need tingimata lineaarselt sõltuvad.

Maatriksi auaste(tähistatud auastmega( A)) on selle vektorite süsteemi aste, millest see koosneb. Kuigi mis tahes maatriksit saab esitada kahel viisil (veeru- või reavektorid), ei mõjuta see järjestuse väärtust, sest

1.14. Pöördmaatriks

Ruutmaatriks A nimetatakse mitte-degeneratiivseks, kui sellel on kordumatu vastupidine maatriks A-1 määratud tingimustega

A.A. −1 = A −1 A = I.

Kõigi maatriksite jaoks ei eksisteeri pöördmaatriksit. Mittedegenereerumise vajalik ja piisav tingimus on

det( A) ≠ 0 või auaste( A) = N.

Maatriksi inversioon on keeruline protseduur, mille jaoks on olemas spetsiaalsed programmid. Näiteks

Riis. 17 Maatriksi inversioon

Toome välja kõige lihtsama juhtumi – 2×2 maatriksi – valemid

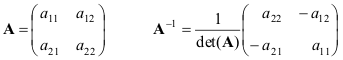
Kui maatriksid A Ja B on siis mitte-mandunud

(AB) −1 = B −1 A −1 .

1.15. Pseudoinversne maatriks

Kui maatriks A on ainsuses ja pöördmaatriksit ei eksisteeri, siis mõnel juhul võite kasutada pseudoinversne maatriks, mis on defineeritud kui selline maatriks A+ see

A.A. + A = A.

Pseudoinversne maatriks pole ainus ja selle vorm sõltub ehitusmeetodist. Näiteks ristkülikukujulise maatriksi jaoks võite kasutada Moore-Penrose'i meetodit.

Kui veergude arv on väiksem kui ridade arv, siis

A + =(A t A) −1 A t

Näiteks

Riis. 17a Maatriksi pseudoinversioon

Kui veergude arv on suurem kui ridade arv, siis

A + =A t ( A.A. t) −1

1.16. Vektori korrutamine maatriksiga

Vektor x saab korrutada maatriksiga A sobiv suurus. Sel juhul korrutatakse veeruvektor paremal Ax, ja vektori rida on vasakul x t A. Kui vektori mõõde J ja maatriksi mõõde I× J siis on tulemuseks mõõtmevektor I. Näiteks

Riis. 18 Vektori korrutamine maatriksiga

Kui maatriks A- ruut ( I× I), siis vektor y = Ax on sama mõõtmega kui x. See on ilmne

A(α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Seetõttu võib maatrikseid pidada vektorite lineaarseteks teisendusteks. Eelkõige Ix = x, Ox = 0 .

2. Lisainfo

2.1. Lineaarvõrrandisüsteemid

Lase A- maatriksi suurus I× J, A b- mõõtmete vektor J. Mõelge võrrandile

Ax = b

vektori suhtes x, mõõtmed I. Põhimõtteliselt on see süsteem I lineaarvõrrandid J teadmata x 1 ,...,x J. Lahendus on olemas siis ja ainult siis

rank( A) = auaste( B) = R,

Kus B on laiendatud mõõtmete maatriks I×( J+1), mis koosneb maatriksist A, mida täiendab veerg b, B = (A b). Vastasel juhul on võrrandid vastuolulised.

Kui R = I = J, siis on lahendus ainulaadne

x = A −1 b.

Kui R < I, siis on palju erinevaid lahendusi, mida saab väljendada läbi lineaarse kombinatsiooni J−R vektorid. Homogeensete võrrandite süsteem Ax = 0 ruutmaatriksiga A (N× N) omab mittetriviaalset lahendust ( x ≠ 0 ) siis ja ainult siis, kui det( A) = 0. Kui R= rank( A)<N, siis neid on N−R lineaarselt sõltumatud lahendused.

2.2. Bilineaarsed ja ruutvormid

Kui A on ruutmaatriks ja x Ja y- vastava mõõtme vektor, seejärel vormi skalaarkorrutis x t Ah helistas bilineaarne maatriksiga määratletud vorm A. Kell x = y väljendus x t Ax helistas ruutkeskne vormi.

2.3. Positiivsed kindlad maatriksid

Ruutmaatriks A helistas positiivne kindel, kui mis tahes nullist erineva vektori korral x ≠ 0 ,

x t Ax > 0.

Sarnaselt määratletud negatiivne (x t Ax < 0), mittenegatiivne (x t Ax≥ 0) ja negatiivne (x t Ax≤ 0) teatud maatriksid.

2.4. Cholesky lagunemine

Kui sümmeetriline maatriks A on positiivne kindel, siis on olemas ainulaadne kolmnurkmaatriks U positiivsete elementidega, mille jaoks

A = U t U.

Näiteks

Riis. 19 Cholesky lagunemine

2.5. Polaarne lagunemine

Lase A on mõõtmete mitteainsuse ruutmaatriks N× N. Siis on ainulaadne polaarne esitus

A = S.R.

Kus S on mittenegatiivne sümmeetriline maatriks ja R on ortogonaalne maatriks. Maatriksid S Ja R saab selgelt määratleda:

S 2 = A.A. t või S = (A.A. t) ½ ja R = S −1 A = (A.A. t) −½ A.

Näiteks

Riis. 20 Polaarne lagunemine

Kui maatriks A on degenereerunud, siis lagunemine pole ainulaadne - nimelt: S ikka üksi, aga R võibolla palju. Polaarne lagunemine esindab maatriksit A kompressiooni/pikenduste kombinatsioonina S ja pöörake R.

2.6. Omavektorid ja omaväärtused

Lase A on ruutmaatriks. Vektor v helistas omavektor maatriksid A, Kui

Av = λ v,

kus kutsutakse arvu λ omaväärtus maatriksid A. Seega teisendus, mille maatriks teostab A vektori kohal v, taandub lihtsale venitamisele või kokkusurumisele koefitsiendiga λ. Omavektor määratakse kuni korrutamiseni konstandiga α ≠ 0, st. Kui v on omavektor, siis α v- ka omavektor.

2.7. Omaväärtused

Maatriksi juures A, mõõde ( N× N) ei saa olla suurem kui N omaväärtused. Nad rahuldavad iseloomulik võrrand

det( A − λ I) = 0,

mis on algebraline võrrand N- järjekorras. Täpsemalt, 2 × 2 maatriksi puhul on iseloomuliku võrrandi vorm

Näiteks

Riis. 21 Omaväärtused

Omaväärtuste komplekt λ 1 ,..., λ N maatriksid A helistas spekter A.

Spektril on erinevad omadused. Eelkõige

det( A) = λ 1 ×... × λ N,Sp( A) = λ 1 +...+λ N.

Suvalise maatriksi omaväärtused võivad olla kompleksarvud, kuid kui maatriks on sümmeetriline ( A t = A), siis on selle omaväärtused reaalsed.

2.8. Omavektorid

Maatriksi juures A, mõõde ( N× N) ei saa olla suurem kui N omavektorid, millest igaüks vastab oma omaväärtusele. Omavektori määramiseks v n vaja lahendada homogeensete võrrandite süsteem

(A − λ n I)v n = 0 .

Sellel on mittetriviaalne lahendus, kuna det( A -λ n I) = 0.

Näiteks

Riis. 22 omavektorit

Sümmeetrilise maatriksi omavektorid on ortogonaalsed.

Omaväärtused (arvud) ja omavektorid.
Näited lahendustest

Ole sina ise

Mõlemast võrrandist järeldub, et .

Paneme siis: .

Selle tulemusena: – teine ​​omavektor.

Kordame olulised punktid lahendused:

– saadud süsteemil on kindlasti üldlahend (võrrandid on lineaarselt sõltuvad);

– valime “y” nii, et see oleks täisarv ja esimene “x” koordinaat oleks täisarv, positiivne ja võimalikult väike.

– kontrollime, et konkreetne lahendus rahuldaks süsteemi iga võrrandit.

Vastus .

Vahepealseid “kontrollpunkte” oli päris piisavalt, nii et võrdsuse kontrollimine on põhimõtteliselt tarbetu.

Erinevates teabeallikates kirjutatakse omavektorite koordinaadid sageli mitte veergudesse, vaid ridadesse, näiteks: (ja ausalt öeldes olen ma ise harjunud neid ridadena üles kirjutama). See valik on vastuvõetav, kuid teemat silmas pidades lineaarsed teisendused tehniliselt mugavam kasutada veeruvektorid.

Võib-olla tundus lahendus teile väga pikk, kuid seda ainult seetõttu, et kommenteerisin esimest näidet väga üksikasjalikult.

Näide 2

Maatriksid

Teeme omal käel trenni! Ligikaudne näide lõpuülesandest tunni lõpus.

Mõnikord peate tegema lisaülesanne, nimelt:

kirjutage kanooniline maatriksi dekomponeerimine

Mis see on?

Kui maatriksi omavektorid moodustavad alusel, siis saab seda esitada järgmiselt:

Kus on omavektorite koordinaatidest koosnev maatriks, – diagonaal maatriks vastavate omaväärtustega.

Seda maatriksi lagunemist nimetatakse kanooniline või diagonaal.

Vaatame esimese näite maatriksit. Selle omavektorid lineaarselt sõltumatu(mittekollineaarne) ja moodustavad aluse. Loome nende koordinaatide maatriksi:

Sees põhidiagonaal maatriksid sobivas järjekorras omaväärtused asuvad ja ülejäänud elemendid on võrdsed nulliga:
– Rõhutan veel kord järjestuse tähtsust: “kaks” vastab 1. vektorile ja asub seetõttu 1. veerus, “kolm” – 2. vektoris.

Kasutades leidmiseks tavalist algoritmi pöördmaatriks või Gaussi-Jordaania meetod leiame . Ei, see pole kirjaviga! - teie ees on haruldane sündmus, nagu päikesevarjutus, kui vastupidine juhtum langes kokku algse maatriksiga.

Jääb üle kirjutada maatriksi kanooniline lagunemine:

Süsteemi saab lahendada elementaarsete teisenduste abil ja järgmistes näidetes kasutame seda meetodit. Kuid siin töötab "kooli" meetod palju kiiremini. 3. võrrandist väljendame: – asendame teise võrrandiga:

Kuna esimene koordinaat on null, saame igast võrrandist süsteemi, millest järeldub, et .

Ja jälle pöörake tähelepanu lineaarse seose kohustuslikule olemasolule. Kui saadakse vaid triviaalne lahendus , siis leiti kas omaväärtus valesti või kompileeriti/lahendati süsteem veaga.

Kompaktsed koordinaadid annavad väärtuse

Omavektor:

Ja veel kord kontrollime, kas lahendus on leitud rahuldab süsteemi iga võrrandi. Järgmistes lõikudes ja järgnevates ülesannetes soovitan seda soovi võtta kui kohustuslikku reeglit.

2) Omaväärtuse jaoks saame sama põhimõtet kasutades järgmise süsteemi:

Süsteemi 2. võrrandist väljendame: – asendame kolmanda võrrandiga:

Kuna “zeta” koordinaat on võrdne nulliga, saame igast võrrandist süsteemi, mille lineaarne sõltuvus järgneb.

Lase

Kontrollides, kas lahendus rahuldab süsteemi iga võrrandi.

Seega on omavektor: .

3) Ja lõpuks, süsteem vastab omaväärtusele:

Teine võrrand näeb välja kõige lihtsam, seega väljendame seda ja asendame selle 1. ja 3. võrrandiga:

Kõik on korras – on tekkinud lineaarne seos, mille asendame väljendiga:

Selle tulemusena väljendati "x" ja "y" läbi "z": . Praktikas ei ole vaja täpselt selliseid suhteid saavutada, mõnel juhul on mugavam väljendada nii läbi kui ka läbi . Või isegi "treeni" - näiteks "X" kuni "I" ja "I" kuni "Z"

Paneme siis:

Kontrollime, kas lahendus on leitud rahuldab süsteemi iga võrrandi ja kirjutab kolmanda omavektori

Vastus: omavektorid:

Geomeetriliselt määratlevad need vektorid kolm erinevat ruumisuunda ("edasi-tagasi"), mille järgi lineaarne teisendus teisendab nullist erinevad vektorid (omavektorid) kollineaarseteks vektoriteks.

Kui tingimus nõudis kanoonilise lagunemise leidmist, siis siin on see võimalik, sest erinevad omaväärtused vastavad erinevatele lineaarselt sõltumatutele omavektoritele. Maatriksi tegemine nende koordinaatide järgi, diagonaalmaatriks alates asjakohane omaväärtusi ja leida pöördmaatriks .

Kui tingimusel peate kirjutama lineaarne teisendusmaatriks omavektorite baasil, siis anname vastuse vormis . Erinevus on ja erinevus on märkimisväärne! Kuna see maatriks on "de" maatriks.

Probleem rohkemaga lihtsad arvutused Sest sõltumatu otsus:

Näide 5

Leidke maatriksiga antud lineaarse teisenduse omavektorid

Enda arvude leidmisel proovige mitte minna 3. astme polünoomini. Lisaks võivad teie süsteemilahendused minu lahendustest erineda – siin pole kindlust; ja leitud vektorid võivad näidisvektoritest erineda kuni nende vastavate koordinaatide proportsionaalsuseni. Näiteks ja. Esteetiliselt meeldivam on vastus vormis esitada, kuid see on okei, kui peatute teise variandi juures. Siiski on kõigel mõistlikud piirid, versioon ei näe enam kuigi hea välja.

Ülesande ligikaudne lõplik näidis õppetunni lõpus.

Kuidas lahendada ülesanne mitme omaväärtuse korral?

Üldine algoritm jääb samaks, kuid sellel on oma eripärad ja mõned lahenduse osad on soovitatav hoida rangemas akadeemilises stiilis:

Näide 6

Leidke omaväärtused ja omavektorid

Lahendus

Muidugi kasutame suurepärast esimest veergu suurtähtedega:

Ja pärast ruuttrinoomi faktoorimist:

Selle tulemusena saadakse omaväärtused, millest kaks on mitmekordsed.

Leiame omavektorid:

1) Käsitleme üksiksõdurit "lihtsustatud" skeemi järgi:

Kahest viimasest võrrandist on selgelt näha võrdsus, mis ilmselt tuleks asendada süsteemi 1. võrrandiga:

Te ei leia paremat kombinatsiooni:
Omavektor:

2-3) Nüüd eemaldame paar vahtkonda. Sel juhul võib see selguda kas kaks või üks omavektor. Olenemata juurte paljususest asendame väärtuse determinandiga mis toob meile järgmise homogeenne lineaarvõrrandisüsteem:

Omavektorid on täpselt vektorid
põhiline lahenduste süsteem

Tegelikult ei teinud me terve õppetunni jooksul muud, kui leidsime põhisüsteemi vektorid. Lihtsalt praegu ei olnud see termin eriti nõutav. Muide, need nutikad õpilased, kes kamuflaažiülikondades teemast mööda lasid homogeensed võrrandid, on sunnitud seda nüüd suitsetama.

Ainus tegevus oli lisaliinide eemaldamine. Tulemuseks on üks-kolm maatriks, mille keskel on formaalne "samm".
– põhimuutuja, – vabad muutujad. Seega on kaks vaba muutujat on ka kaks põhisüsteemi vektorit.

Avaldame põhimuutujat vabade muutujatena: . Nulltegur X-i ees võimaldab sellel võtta absoluutselt mis tahes väärtusi (mis on võrrandisüsteemist selgelt nähtav).

Selle ülesande kontekstis on mugavam kirjutada üldlahendus mitte ritta, vaid veergu:

Paar vastab omavektorile:
Paar vastab omavektorile:

Märkus : kogenud lugejad saavad need vektorid valida suuliselt – lihtsalt süsteemi analüüsides , kuid siin on vaja teadmisi: on kolm muutujat, süsteemimaatriksi auaste- üks, mis tähendab põhimõtteline otsustussüsteem koosneb 3 – 1 = 2 vektorist. Leitud vektorid on aga selgelt nähtavad ka ilma selle teadmiseta, puhtalt intuitiivsel tasandil. Sel juhul kirjutatakse kolmas vektor veelgi “ilusamalt”: . Hoiatan aga, et teises näites ei pruugi lihtne valik olla võimalik, mistõttu on klausel mõeldud kogenud inimestele. Lisaks, miks mitte võtta näiteks kolmandat vektorit? Lõppude lõpuks rahuldavad selle koordinaadid ka süsteemi iga võrrandit ja vektoreid lineaarselt sõltumatu. See valik on põhimõtteliselt sobiv, kuid "kõver", kuna "muu" vektor on põhisüsteemi vektorite lineaarne kombinatsioon.

Vastus: omaväärtused: , omavektorid:

Sarnane näide sõltumatu lahenduse jaoks:

Näide 7

Leidke omaväärtused ja omavektorid

Lõpliku kavandi ligikaudne näidis õppetunni lõpus.

Tuleb märkida, et nii 6. kui ka 7. näites saadakse lineaarselt sõltumatute omavektorite kolmik ja seetõttu on esialgne maatriks kanoonilises lagunemises esindatav. Kuid selliseid vaarikaid ei juhtu kõigil juhtudel:

Näide 8

Lahendus: Loome ja lahendame tunnusvõrrandi:

Laiendame esimeses veerus olevat determinanti:

Täiendavaid lihtsustusi teostame vastavalt vaadeldavale meetodile, vältides kolmanda astme polünoomi:

- omaväärtused.

Leiame omavektorid:

1) Juurega pole raskusi:

Ärge üllatuge, lisaks komplektile on kasutusel ka muutujad - siin pole vahet.

3. võrrandist väljendame selle ja asendame selle 1. ja 2. võrrandiga:

Mõlemast võrrandist järeldub:

Lase siis:

2-3) Mitme väärtuse korral saame süsteemi .

Kirjutame üles süsteemi maatriksi ja viime elementaarsete teisenduste abil astmelisele kujule:

www.sait võimaldab teil leida. Sait teostab arvutuse. Mõne sekundi pärast annab server õige lahenduse. Maatriksi iseloomulik võrrand on algebraline avaldis, mis leitakse determinandi arvutamise reeglit kasutades maatriksid maatriksid, samas kui põhidiagonaalis on diagonaalelementide ja muutuja väärtustes erinevusi. Arvutamisel maatriksi tunnusvõrrand võrgus, iga element maatriksid korrutatakse vastavate muude elementidega maatriksid. Otsige režiimis võrgus võimalik ainult ruudu jaoks maatriksid. Operatsiooni leidmine maatriksi tunnusvõrrand võrgus taandub elementide korrutise algebralise summa arvutamiseks maatriksid determinandi leidmise tulemusena maatriksid, ainult kindlaksmääramise eesmärgil maatriksi tunnusvõrrand võrgus. Sellel operatsioonil on teoorias eriline koht maatriksid, võimaldab juurte abil leida omaväärtusi ja vektoreid. Ülesanne leida maatriksi tunnusvõrrand võrgus koosneb korrutavatest elementidest maatriksid millele järgneb nende toodete summeerimine teatud reegli järgi. www.sait leiab maatriksi iseloomulik võrrand antud dimensioon režiimis võrgus. Arvutamine maatriksi tunnusvõrrand võrgus selle dimensiooni arvestades on see numbriliste või sümboolsete koefitsientidega polünoomi leidmine, mis leitakse vastavalt determinandi arvutamise reeglile maatriksid- vastavate elementide korrutiste summana maatriksid, ainult kindlaksmääramise eesmärgil maatriksi tunnusvõrrand võrgus. Polünoomi leidmine ruutsuuruse muutuja suhtes maatriksid, määratlusena maatriksi iseloomulik võrrand, teoreetiliselt levinud maatriksid. Polünoomi juurte tähendus maatriksi tunnusvõrrand võrgus kasutatakse omavektorite ja omaväärtuste määramiseks maatriksid. Pealegi, kui determinant maatriksid on siis võrdne nulliga maatriksi karakteristlik võrrand erinevalt vastupidisest on endiselt olemas maatriksid. Selleks, et arvutada maatriksi iseloomulik võrrand või leida mitu korraga maatriksite tunnusvõrrandid, peate kulutama palju aega ja vaeva, samas kui meie server leiab mõne sekundiga võrgumaatriksi tunnusvõrrand. Sel juhul vastus leidmisele maatriksi tunnusvõrrand võrgus on õige ja piisava täpsusega, isegi kui numbrid leidmisel maatriksi tunnusvõrrand võrgus saab olema irratsionaalne. Veebilehel www.sait märkide sisestamine on elementides lubatud maatriksid, see tähendab võrgumaatriksi tunnusvõrrand saab arvutamisel esitada üldisel sümboolsel kujul maatriksi iseloomulik võrrand võrgus. Saadud vastust on kasulik kontrollida leidmisülesande lahendamisel maatriksi tunnusvõrrand võrgus saidi kasutades www.sait. Polünoomi arvutamise toimingu tegemisel - maatriksi karakteristlik võrrand, peate selle probleemi lahendamisel olema ettevaatlik ja äärmiselt keskendunud. Meie sait omakorda aitab teil kontrollida oma otsust sellel teemal maatriksi tunnusvõrrand võrgus. Kui teil pole aega lahendatud probleemide pikaks kontrollimiseks, siis www.sait on kindlasti mugav tööriist otsimisel ja arvutamisel maatriksi tunnusvõrrand võrgus.

Juhised

Arvu k nimetatakse maatriksi A omaväärtuseks (arvuks), kui on olemas vektor x, mille korral Ax=kx. (1) Sel juhul nimetatakse vektorit x maatriksi A omavektoriks, mis vastab arvule k Ruumis R^n (vt joonis 1) on maatriksil A kujund nagu joonisel.

On vaja püstitada ülesanne leida maatriksi A vektorid. Olgu omavektor x antud koordinaatidega. Maatriksi kujul kirjutatakse see veerumaatriksina, mis mugavuse huvides tuleks esitada transponeeritud reana. X=(x1,x2,…,xn)^T Põhineb (1), Ax-khx=0 või Ax-kEx=0, kus E on identsusmaatriks (ühed põhidiagonaalil, kõik muud elemendid on nullid). ). Siis (A-kE)x=0. (2)

Lineaarsete homogeensete algebraliste võrrandite avaldisel (2) on nullist erinev lahend (omavektor). Seetõttu on süsteemi (2) põhideterminant võrdne nulliga, st |A-kE|=0. (3) Omaväärtuse k viimast võrdsust nimetatakse maatriksi A karakteristikuks ja laiendatud kujul on sellel kuju (vt joonis 2).

Asendades tunnusvõrrandi juure k süsteemiks (2), homogeenseks lineaarvõrrandisüsteemiks singulaarmaatriksiga (selle determinant on null). Selle süsteemi iga nullist erinev lahend on maatriksi A omavektor, mis vastab antud omaväärtusele k (st karakteristiku võrrandi juur).

Näide. Leidke maatriksi A omaväärtused ja vektorid (vt joonis 3). Iseloomulik võrrand on esitatud joonisel fig. 3. Laiendage determinanti ja leidke maatriksi omaväärtused, milleks on antud võrrand (3-k)(-1-k)-5=0, (k-3)(k+1)-5=0 , k^2-2k -8=0 Selle juured on k1=4, k2=-2

a) K1=4-le vastavad omavektorid leitakse süsteemi (A-4kE)х=0 lahendamisel. Sel juhul on vaja ainult ühte selle võrrandit, kuna süsteemi determinant on ilmselgelt võrdne nulliga. Kui panna x=(x1, x2)^T, siis on süsteemi esimene võrrand (1-4)x1+x2=0, -3x1+x2=0. Kui eeldame, et x1=1 (kuid mitte null), siis x2=3. Kuna singulaarmaatriksiga homogeensel süsteemil on nii palju nullist erinevaid lahendeid kui soovitakse, siis kogu esimesele omaväärtusele vastav omavektorite hulk x =C1(1, 3), C1=const.

b) Leia omavektorid, mis vastavad k2=-2-le. Süsteemi (A+2kE)x=0 lahendamisel on selle esimene võrrand (3+2)x1+x2=0, 5x1+x2=0 Kui paneme x1=1, siis x2=-5. Vastavad omavektorid x =C2(1, 3), C2=konst. Antud maatriksi kõigi omavektorite koguhulk: x = C1(1, 3)+ C2(1, 3).

Allikad:

• Piskunov N.S. Diferentsiaal- ja integraalarvutus. M., 1976, - 576 lk.
• leida omaväärtusi ja maatriksvektoreid

Lineaarvõrrandisüsteemidega töötamisel kasutatakse laialdaselt maatrikseid, mis on andmete salvestamise tabelivorm. Veelgi enam, võrrandite arv määrab maatriksi ridade arvu ja muutujate arv selle veergude järjekorra. Selle tulemusena taandatakse lineaarsete süsteemide lahendamine maatriksitega tehtavateks toiminguteks, millest üks on maatriksi omaväärtuste leidmine. Nende arvutamine toimub iseloomuliku võrrandi abil. Omaväärtusi saab määrata ruutmaatriksi jaoks, mille suurus on m.

Juhised

Kirjutage üles antud ruut A. Selle omaväärtuste leidmiseks kasutage lineaarse homogeense süsteemi mittetriviaalse lahenduse tingimusest tulenevat karakteristlikku võrrandit, mida antud juhul kujutab ruutmaatriks. Nagu Cramerist järeldub, on lahendus olemas ainult siis, kui selle determinant on võrdne nulliga. Seega saame kirjutada võrrandi | A - λE | = 0, kus A on antud väärtus, λ on nõutavad arvud, E on identsusmaatriks, milles kõik põhidiagonaali elemendid on võrdsed ühega ja ülejäänud on võrdsed nulliga.

Korrutage soovitud muutuja λ identiteedimaatriksiga E, mis on sama mõõtmega kui antud algne A. Tehe tulemuseks on maatriks, kus λ väärtused paiknevad piki põhidiagonaali, ülejäänud elemendid jäävad nulliks .