This uncertainty is “served” second wonderful limit , and in the second part of that lesson we looked in great detail at standard examples of solutions that are found in practice in most cases. Now the picture with the exponents will be completed, in addition, the final tasks of the lesson will be devoted to “false” limits, in which it SEEMS that it is necessary to apply the 2nd wonderful limit, although this is not at all the case.
The disadvantage of the two working formulas for the 2nd remarkable limit is that the argument must tend to “plus infinity” or to zero. But what if the argument tends to a different number?
A universal formula comes to the rescue (which is actually a consequence of the second remarkable limit):
Uncertainty can be eliminated using the formula:
Somewhere I think I already explained what the square brackets mean. Nothing special, brackets are just brackets. They are usually used to highlight mathematical notation more clearly.
Let us highlight the essential points of the formula:
1) It's about only about certainty and nothing else.
2) The “x” argument can tend to arbitrary value(and not just to zero or), in particular, to “minus infinity” or to anyone finite number.
Using this formula you can solve all the examples in the lesson. Wonderful Limits, which belong to the 2nd remarkable limit. For example, let's calculate the limit:
In this case 
, and according to the formula 
:
True, I don’t recommend doing this; the tradition is to still use the “usual” design of the solution, if it can be applied. However using the formula it is very convenient to check"classical" examples to the 2nd remarkable limit.
All this is good and correct, but now there are more interesting shots in the frame:
Example 18
Calculate limit 
At the first step, I will not tire of repeating, we substitute the value of “x” into the expression under the limit sign. What if there is no uncertainty at all? It happens! But not this time. Substituting the “three”, we come to the conclusion that there is uncertainty here
We use the formula
In order not to drag the letter “e” around with you and not to make it smaller, the indicator 
It’s more convenient to calculate separately:
In this case: 
Thus:
From the point of view of calculation technology, everything is routine: first we reduce the first term to a common denominator, then we take out the constants and carry out reductions, getting rid of the 0:0 uncertainty.
As a result: 
Promised gift with logarithm difference and uncertainty:
Example 19
Calculate limit
First the complete solution, then comments: 
(1)-(2) In the first two steps we use the formulas 
. U complex derivatives we “fall apart” logarithms, but here, on the contrary, they need to be “assembled”.
(3) Move the limit icon below the logarithm. This can be done because this logarithm continuous to "minus infinity". In addition, the limit refers to the “filling” of the logarithm.
(4)-(5) Standard technique discussed in the basic lesson about wonderful limits, we transform the uncertainty to the form .
(6) We use the formula .
(7) Exponential and logarithmic functions are mutually inverse functions, so both “e” and the logarithm can be removed. Indeed, according to the property of the logarithm: . We add the minus before the fraction to the denominator: 
(8) No comments =)
The type of limit considered is not so rare; I found 30-40 examples.
Example 20
Calculate limit 
This is an example for independent decision. In addition to using the formula, you can represent the limit as 
and by replacement reduce the solution to the case 
.
In conclusion, let’s look at the “fake” limits.
Let's return to uncertainty. This uncertainty not always can be reduced to uncertainty and use the second remarkable limit or corollary formula. The transformation is feasible if numerator and denominator of the base - equivalent infinitely large functions. For example: .
Let's take a break from the indicator and calculate the limit of the base: 
In the limit obtained unit, which means the numerator and denominator not just of the same order of growth, but also equivalent. In class Remarkable limits. Examples of solutions We easily reduced this example to uncertainty and got the answer.
You can come up with a lot of similar limits:
etc.
The fractions of these examples are united by the above feature: . In other cases, if there is uncertainty 2nd remarkable limit is not applicable.
Example 21
Find limits
No matter how hard you try, uncertainty cannot be transformed into uncertainty
Here are the numerators and denominators of the bases same order of growth, but not equivalent: 
.
Thus, the second remarkable limit and, especially the formula, CANNOT BE APPLIED.
! Note: Not to be confused with Example #18, in which the numerator and denominator of the base are not equivalent. There is ready-made uncertainty, but here we are talking about uncertainty.
The method for solving “fake” limits is simple and sign: you need a numerator and a denominator grounds divide by “x” to the highest degree (regardless of the exponent):
If the numerator and denominator of the base are of different order of growth, then the solution is exactly the same:
Example 22
Find limits 
These are short examples for self-study
Sometimes there may be no uncertainty at all:
Such tricks are especially loved by the compilers of Kuznetsov’s collection. That is why it is very important to ALWAYS substitute “x” into the expression under the limit sign in the first step!
Example 2
Major degree of numerator: 2; highest degree of denominator: 3.
:
Example 4
Divide the numerator and denominator by :
Note
: the very last action was to multiply the numerator and denominator by to get rid of irrationality in the denominator.
Example 6
Divide the numerator and denominator by :
Example 8
Divide the numerator and denominator by :
Note
: term tend to zero slower than , That's why is the “main” zero of the denominator.
.
Example 22
Note
: endlessly small function
tends to zero slower than , so the “larger” zero of the denominator plays a decisive role:
The derivative of the function does not fall far, and in the case of L'Hopital's rules it falls exactly in the same place where the original function falls. This circumstance helps in revealing uncertainties of the form 0/0 or ∞/∞ and some other uncertainties that arise when calculating limit the relationship of two infinitesimal or infinitely large functions. The calculation is greatly simplified using this rule (actually two rules and notes to them):
As the formula above shows, when calculating the limit of the ratio of two infinitesimal or infinitely large functions, the limit of the ratio of two functions can be replaced by the limit of the ratio of their derivatives and thus obtain a certain result.
Let's move on to more precise formulations of L'Hopital's rules.
L'Hopital's rule for the case of the limit of two infinitesimal quantities. Let the functions f(x) And g(x a. And at the very point a a derivative of a function g(x) is not zero ( g"(x a are equal to each other and equal to zero:
.
L'Hopital's rule for the case of the limit of two infinitely large quantities. Let the functions f(x) And g(x) have derivatives (that is, differentiable) in some neighborhood of the point a. And at the very point a they may not have derivatives. Moreover, in the vicinity of the point a derivative of a function g(x) is not zero ( g"(x)≠0) and the limits of these functions as x tends to the value of the function at the point a are equal to each other and equal to infinity:
.
Then the limit of the ratio of these functions is equal to the limit of the ratio of their derivatives:
In other words, for uncertainties of the form 0/0 or ∞/∞, the limit of the ratio of two functions is equal to the limit of the ratio of their derivatives, if the latter exists (finite, that is, equal to a certain number, or infinite, that is, equal to infinity).
Notes.
1. L'Hopital's rules are also applicable when the functions f(x) And g(x) are not defined when x = a.
2. If, when calculating the limit of the ratio of derivatives of functions f(x) And g(x) we again come to an uncertainty of the form 0/0 or ∞/∞, then L'Hôpital's rules should be applied repeatedly (at least twice).
3. L'Hopital's rules are also applicable when the argument of functions (x) does not tend to a finite number a, and to infinity ( x → ∞).
Uncertainties of other types can also be reduced to uncertainties of the types 0/0 and ∞/∞.
Disclosure of uncertainties of the types “zero divided by zero” and “infinity divided by infinity”
Example 1.
x=2 leads to uncertainty of the form 0/0. Therefore, the derivative of each function is obtained
The derivative of the polynomial was calculated in the numerator, and in the denominator - derivative of a complex logarithmic function. Before the last equal sign, the usual limit, substituting a two instead of an X.
Example 2. Calculate the limit of the ratio of two functions using L'Hopital's rule:
Solution. Substituting a value into a given function x
Example 3. Calculate the limit of the ratio of two functions using L'Hopital's rule:
Solution. Substituting a value into a given function x=0 leads to uncertainty of the form 0/0. Therefore, we calculate the derivatives of the functions in the numerator and denominator and get:
Example 4. Calculate
Solution. Substituting the value x equal to plus infinity into a given function leads to an uncertainty of the form ∞/∞. Therefore, we apply L'Hopital's rule:
Comment. Let's move on to examples in which L'Hopital's rule has to be applied twice, that is, to come to the limit of the ratio of the second derivatives, since the limit of the ratio of the first derivatives is an uncertainty of the form 0/0 or ∞/∞.
Uncovering uncertainties of the form “zero times infinity”
Example 12. Calculate
.
Solution. We get
This example uses the trigonometric identity.
Disclosure of uncertainties of the types "zero to the power of zero", "infinity to the power of zero" and "one to the power of infinity"
Uncertainties of the form , or are usually reduced to the form 0/0 or ∞/∞ by taking the logarithm of a function of the form
To calculate the limit of an expression, you should use the logarithmic identity, a special case of which is the property of the logarithm 
.
Using the logarithmic identity and the property of continuity of a function (to pass the limit sign), the limit should be calculated as follows:
Separately, you should find the limit of the expression in the exponent and build e to the found degree.
Example 13.
Solution. We get
.
.
Example 14. Calculate using L'Hopital's rule
Solution. We get
Calculate the limit of an expression in exponent
.
.
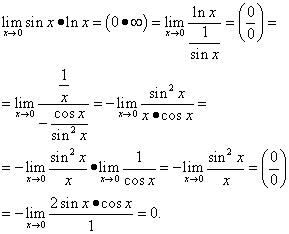Example 15. Calculate using L'Hopital's rule
In the previous article we talked about how to correctly calculate the limits of elementary functions. If we take more complex functions, then we will have expressions with an undefined value in our calculations. They are called uncertainties.
The following main types of uncertainties are distinguished:
- Divide 0 by 0 0 0 ;
- Dividing one infinity by another ∞ ∞;
- infinity raised to the zero power ∞ 0 .
0 raised to the zero power 0 0 ;
We have listed all the main uncertainties. Other expressions may take on finite or infinite values under different conditions and therefore cannot be considered uncertainties.
Uncovering Uncertainties
Uncertainty can be resolved by:
- By simplifying the form of the function (using abbreviated multiplication formulas, trigonometric formulas, additional multiplication by conjugate expressions and subsequent reduction, etc.);
With the help of wonderful limits;
Using L'Hopital's rule;
By replacing one infinitesimal expression with its equivalent expression (as a rule, this action is performed using a table of infinitesimal expressions).
All the information presented above can be clearly presented in the form of a table. On the left side it shows the type of uncertainty, on the right - a suitable method for revealing it (finding the limit). This table is very convenient to use in calculations related to finding limits.
| Uncertainty | Uncertainty Disclosure Method |
| 1. Divide 0 by 0 | Transformation and subsequent simplification of an expression. If the expression is sin (k x) k x or k x sin (k x) then you need to use the first remarkable limit. If this solution is not suitable, we use L'Hopital's rule or a table of equivalent infinitesimal expressions |
| 2. Dividing infinity by infinity | Transform and simplify an expression or use L'Hopital's rule |
| 3. Multiplying zero by infinity or finding the difference between two infinities | Conversion to 0 0 or ∞ ∞ followed by application of L'Hopital's rule |
| 4. Unit to the power of infinity | Using the Second Great Limit |
| 5. Raising zero or infinity to the zero power | Taking the logarithm of an expression using the equality lim x → x 0 ln (f (x)) = ln lim x → x 0 f (x) |
Let's look at a couple of problems. These examples are quite simple: in them the answer is obtained immediately after substituting the values and there is no uncertainty.
Example 1
Calculate the limit lim x → 1 x 3 + 3 x - 1 x 5 + 3 .
Solution
We perform value substitution and get the answer.
lim x → 1 x 3 + 3 x - 1 x 5 + 3 = 1 3 + 3 1 - 1 1 5 + 3 = 3 4 = 3 2
Answer: lim x → 1 x 3 + 3 x - 1 x 5 + 3 = 3 2 .
Example 2
Calculate the limit lim x → 0 (x 2 + 2 , 5) 1 x 2 .
Solution
We have an exponential power function, into the base of which we need to substitute x = 0.
(x 2 + 2, 5) x = 0 = 0 2 + 2, 5 = 2, 5
This means we can transform the limit into the following expression:
lim x → 0 (x 2 + 2, 5) 1 x 2 = lim x → 0 2, 5 1 x 2
Now let's look at the indicator - the power function 1 x 2 = x - 2. Let's look at the table of limits for power functions with an exponent less than zero and we get the following: lim x → 0 + 0 1 x 2 = lim x → 0 + 0 x - 2 = + ∞ and lim x → 0 + 0 1 x 2 = lim x → 0 + 0 x - 2 = + ∞
Thus, we can write that lim x → 0 (x 2 + 2, 5) 1 x 2 = lim x → 0 2, 5 1 x 2 = 2, 5 + ∞.
Now we take the table of limits of exponential functions with bases greater than 0, and we get:
lim x → 0 (x 2 + 2, 5) 1 x 2 = lim x → 0 2, 5 1 x 2 = 2, 5 + ∞ = + ∞
Answer: lim x → 0 (x 2 + 2 , 5) 1 x 2 = + ∞ .
Example 3
Calculate the limit lim x → 1 x 2 - 1 x - 1 .
Solution
We perform value substitution.
lim x → 1 x 2 - 1 x - 1 = 1 2 - 1 1 - 1 = 0 0
As a result, we ended up with uncertainty. Use the table above to select a solution method. It indicates that you need to simplify the expression.
lim x → 1 x 2 - 1 x - 1 = 0 0 = lim x → 1 (x - 1) (x + 1) x - 1 = = lim x → 1 (x - 1) (x + 1) · (x + 1) x - 1 = lim x → 1 (x + 1) · x - 1 = = 1 + 1 · 1 - 1 = 2 · 0 = 0
As we can see, simplification has led to the revelation of uncertainty.
Answer: lim x → 1 x 2 - 1 x - 1 = 0
Example 4
Calculate the limit lim x → 3 x - 3 12 - x - 6 + x .
Solution
We substitute the value and get the following entry.
lim x → 3 x - 3 12 - x - 6 + x = 3 - 3 12 - 3 - 6 + 3 = 0 9 - 9 = 0 0
We have come to the need to divide zero by zero, which is uncertainty. Let's look at the required solution method in the table - this is simplification and transformation of the expression. Let us additionally multiply the numerator and denominator by the conjugate expression 12 - x + 6 + x:
lim x → 3 x - 3 12 - x - 6 + x = 0 0 = lim x → 3 x - 3 12 - x + 6 + x 12 - x - 6 + x 12 - x + 6 + x
The denominator is multiplied so that you can then use the abbreviated multiplication formula (difference of squares) to perform the reduction.
lim x → 3 x - 3 12 - x + 6 + x 12 - x - 6 + x 12 - x + 6 + x = lim x → 3 x - 3 12 - x + 6 + x 12 - x 2 - 6 + x 2 = lim x → 3 (x - 3) 12 - x + 6 + x 12 - x - (6 + x) = = lim x → 3 (x - 3) 12 - x + 6 + x 6 - 2 x = lim x → 3 (x - 3) 12 - x + 6 + x - 2 (x - 3) = = lim x → 3 12 - x + 6 + x - 2 = 12 - 3 + 6 + 3 - 2 = 9 + 9 - 2 = - 9 = - 3
As we can see, as a result of these actions we were able to get rid of uncertainty.
Answer: lim x → 3 x - 3 12 - x - 6 + x = - 3 .
It is important to note that the multiplication approach is used very often when solving problems like this, so we advise you to remember exactly how this is done.
Example 5
Calculate the limit lim x → 1 x 2 + 2 x - 3 3 x 2 - 5 x + 2 .
Solution
We perform the substitution.
lim x → 1 x 2 + 2 x - 3 3 x 2 - 5 x + 2 = 1 2 + 2 1 - 3 3 1 2 - 5 1 + 2 = 0 0
As a result, we ended up with uncertainty. The recommended way to solve the problem in this case is to simplify the expression. Since at the value of x, equal to one, the numerator and denominator turn to 0, then we can factor them and then reduce them by x - 1, and then the uncertainty will disappear.
We factorize the numerator:
x 2 + 2 x - 3 = 0 D = 2 2 - 4 1 (- 3) = 16 ⇒ x 1 = - 2 - 16 2 = - 3 x 2 = - 2 + 16 2 = 1 ⇒ x 2 + 2 x - 3 = x + 3 x - 1
Now we do the same with the denominator:
3 x 2 - 5 x + 2 = 0 D = - 5 2 - 4 3 2 = 1 ⇒ x 1 = 5 - 1 2 3 = 2 3 x 2 = 5 + 1 2 3 = 1 ⇒ 3 x 2 - 5 x + 3 = 3 x - 2 3 x - 1
We got a limit of the following form:
lim x → 1 x 2 + 2 x - 3 3 x 2 - 5 x + 2 = 0 0 = lim x → 1 x + 3 x - 1 3 x - 2 3 x - 1 = = lim x → 1 x + 3 3 x - 2 3 = 1 + 3 3 1 - 2 3 = 4
As we can see, during the transformation we managed to get rid of uncertainty.
Answer: lim x → 1 x 2 + 2 x - 3 3 x 2 - 5 x + 2 = 4 .
Next we need to consider the cases of limits at infinity from power expressions. If the exponents of these expressions are greater than 0, then the limit at infinity will also be infinite. In this case, the largest degree is of primary importance, and the rest can be ignored.
For example, lim x → ∞ (x 4 + 2 x 3 - 6) = lim x → ∞ x 4 = ∞ or lim x → ∞ x 4 + 4 x 3 + 21 x 2 - 11 5 = lim x → ∞ x 4 5 = ∞.
If under the limit sign we have a fraction with power expressions in the numerator and denominator, then as x → ∞ we have an uncertainty of the form ∞ ∞. To get rid of this uncertainty, we need to divide the numerator and denominator of the fraction by x m a x (m, n). Let us give an example of solving such a problem.
Example 6
Calculate the limit lim x → ∞ x 7 + 2 x 5 - 4 3 x 7 + 12 .
Solution
lim x → ∞ x 7 + 2 x 5 - 4 3 x 7 + 12 = ∞ ∞
The powers of the numerator and denominator are equal to 7. Divide them by x 7 and get:
lim x → ∞ x 7 + 2 x 5 - 4 3 x 7 + 12 = lim x → ∞ x 7 + 2 x 5 - 4 x 7 3 x 7 + 12 x 7 = = lim x → ∞ 1 + 2 x 2 - 4 x 7 3 + 12 x 7 = 1 + 2 ∞ 2 - 4 ∞ 7 3 + 12 ∞ 7 = 1 + 0 - 0 3 + 0 = 1 3
Answer: lim x → ∞ x 7 + 2 x 5 - 4 3 x 7 + 12 = 1 3 .
Example 7
Calculate the limit lim x → ∞ x 8 + 11 3 x 2 + x + 1 .
Solution
lim x → ∞ x 8 + 11 3 x 2 + x + 1 = ∞ ∞
The numerator has a power of 8 3 and the denominator has a power of 2. Let's divide the numerator and denominator by x 8 3:
lim x → ∞ x 8 + 11 3 x 2 + x + 1 = ∞ ∞ = lim x → ∞ x 8 + 11 3 x 8 3 x 2 + x + 1 x 8 3 = = lim x → ∞ 1 + 11 x 8 3 1 x 2 3 + 1 x 5 3 + 1 x 8 3 = 1 + 11 ∞ 3 1 ∞ + 1 ∞ + 1 ∞ = 1 + 0 3 0 + 0 + 0 = 1 0 = ∞
Answer: lim x → ∞ x 8 + 11 3 x 2 + x + 1 = ∞ .
Example 8
Calculate the limit lim x → ∞ x 3 + 2 x 2 - 1 x 10 + 56 x 7 + 12 3 .
Solution
lim x → ∞ x 3 + 2 x 2 - 1 x 10 + 56 x 7 + 12 3 = ∞ ∞
We have a numerator to the power of 3 and a denominator to the power of 10 3 . This means we need to divide the numerator and denominator by x 10 3:
lim x → ∞ x 3 + 2 x 2 - 1 x 10 + 56 x 7 + 12 3 = ∞ ∞ = lim x → ∞ x 3 + 2 x 2 - 1 x 10 3 x 10 + 56 x 7 + 12 3 x 10 3 = = lim x → ∞ 1 x 1 3 + 2 x 4 3 - 1 x 10 3 1 + 56 x 3 + 12 x 10 3 = 1 ∞ + 2 ∞ - 1 ∞ 1 + 56 ∞ + 12 ∞ 3 = 0 + 0 - 0 1 + 0 + 0 3 = 0
Answer: lim x → ∞ x 3 + 2 x 2 - 1 x 10 + 56 x 7 + 12 3 = 0 .
Conclusions
In the case of a ratio limit, there are three main options:
If the degree of the numerator is equal to the degree of the denominator, then the limit will be equal to the ratio of the coefficients of the higher powers.
If the degree of the numerator is greater than the degree of the denominator, then the limit will be equal to infinity.
If the degree of the numerator is less than the degree of the denominator, then the limit will be zero.
We will discuss other methods for disclosing uncertainties in separate articles.
If you notice an error in the text, please highlight it and press Ctrl+Enter
LESSON 20
20.1 DISCLOSURE OF SPECIES UNCERTAINTY
Example 1
Solve limit 
First, let's try to substitute -1 into the fraction: 
In this case, the so-called uncertainty is obtained.
General rule: if the numerator and denominator contain polynomials, and there is uncertainty of the form, then to reveal it you need to factor the numerator and denominator.
To do this, most often you need to solve a quadratic equation and/or use abbreviated multiplication formulas.
Let's factorize the numerator. 
Example 2
Calculate limit 
Let's factor the numerator and denominator.
Numerator: Denominator: 
,
Method of multiplying the numerator and denominator by the conjugate expression
We continue to consider the uncertainty of the form
The next type of limits is similar to the previous type. The only thing, in addition to polynomials, we will add roots.
Example 3
Find the limit 
Multiply the numerator and denominator by the conjugate expression.
20.2 DISCLOSURE OF SPECIES UNCERTAINTY
Now we will consider the group of limits when , and the function is a fraction whose numerator and denominator contain polynomials
Example 4
Calculate limit 
According to our rule, we will try to substitute infinity into the function. What do we get at the top? Infinity. And what happens below? Also infinity. Thus we have what is called species uncertainty. One might think that the answer is ready, but in the general case this is not at all the case, and it is necessary to apply some solution technique, which we will now consider.
How to solve limits of this type?
First we look at the numerator and find the highest power: 
The leading power in the numerator is two.
Now we look at the denominator and also find it to the highest power: 
The highest degree of the denominator is two.
Then we choose the highest power of the numerator and denominator: in this example, they are the same and equal to two.
So, the solution method is as follows: to reveal uncertaintyyou need to divide the numerator and denominator byin the senior degree.
Divide the numerator and denominator by 
Here it is, the answer, and not infinity at all.
What is fundamentally important in the design of a decision?
First, we indicate uncertainty, if any.
Secondly, it is advisable to interrupt the solution for intermediate explanations. I usually use the sign, it does not have any mathematical meaning, but means that the solution is interrupted for an intermediate explanation.
Thirdly, in the limit it is advisable to mark what is going where. When the work is drawn up by hand, it is more convenient to do it this way: 
It is better to use a simple pencil for notes.
Of course, you don’t have to do any of this, but then, perhaps, the teacher will point out shortcomings in the solution or start asking additional questions about the assignment. Do you need it?
Example 5
Find the limit 
Again in the numerator and denominator we find in the highest degree: 
Maximum degree in the numerator: 3 Maximum degree in the denominator: 4 Select greatest value, in this case four. According to our algorithm, to reveal uncertainty, we divide the numerator and denominator by. The complete assignment might look like this:
Example 6
Find the limit 
Maximum degree of “X” in the numerator: 2 Maximum degree of “X” in the denominator: 1 (can be written as) To reveal uncertainty, it is necessary to divide the numerator and denominator by. The final solution might look like this:
Divide the numerator and denominator by
Notation does not mean division by zero (you cannot divide by zero), but division by an infinitesimal number.
Thus, by uncovering species uncertainty, we may be able to final number, zero or infinity.
PRACTICUM 20
TASK N 1
Solution: If instead of the variable we put the value 7 to which it tends, then we get an uncertainty of the form 
TASK N 2Topic: Disclosure of uncertainty of the “zero to zero” type
Solution: If instead of a variable we put the value 0 to which it tends, then we get an uncertainty of the form
TASK N 3Topic: Disclosure of uncertainty of the “zero to zero” type
Solution: If instead of the variable we put the value 6 to which it tends, then we get uncertainty of the form
TASK N 4
Solution: Because 
And 
TASK N 5Topic: Disclosure of uncertainty of the form "infinity to infinity"
Solution: Because 
And 
then there is uncertainty of the form. To reveal it, you need to divide each term of the numerator and denominator by. Then, knowing what we get: 
INDEPENDENT WORK 20
TASK N 1Topic: Disclosure of uncertainty of the “zero to zero” type
TASK N 2Topic: Disclosure of uncertainty of the “zero to zero” type
TASK N 3Topic: Disclosure of uncertainty of the “zero to zero” type
TASK N 4Topic: Disclosure of uncertainty of the form "infinity to infinity"
TASK N 5Topic: Disclosure of uncertainty of the form "infinity to infinity" Function limit 
equal...
TASK N 6Topic: Disclosure of uncertainty of the form "infinity to infinity"
Limits give all mathematics students a lot of trouble. To solve a limit, sometimes you have to use a lot of tricks and choose from a variety of solution methods exactly the one that is suitable for a particular example.
In this article we will not help you understand the limits of your capabilities or comprehend the limits of control, but we will try to answer the question: how to understand limits in higher mathematics? Understanding comes with experience, so at the same time we will give several detailed examples of solving limits with explanations.
The concept of limit in mathematics
The first question is: what is this limit and the limit of what? We can talk about the limits of numerical sequences and functions. We are interested in the concept of the limit of a function, since this is what students most often encounter. But first, the most general definition of a limit:
Let's say there is some variable value. If this value in the process of change unlimitedly approaches a certain number a , That a – the limit of this value.
For a function defined in a certain interval f(x)=y such a number is called a limit A , which the function tends to when X , tending to a certain point A . Dot A belongs to the interval on which the function is defined.
It sounds cumbersome, but it is written very simply:
Lim- from English limit- limit.
There is also a geometric explanation for determining the limit, but here we will not delve into the theory, since we are more interested in the practical rather than the theoretical side of the issue. When we say that X tends to some value, this means that the variable does not take on the value of a number, but approaches it infinitely close.
Let's give a specific example. The task is to find the limit.
To solve this example, we substitute the value x=3 into a function. We get:
By the way, if you are interested in basic operations on matrices, read a separate article on this topic.
In examples X can tend to any value. It can be any number or infinity. Here's an example when X tends to infinity:
Intuitively, the larger the number in the denominator, the smaller the value the function will take. So, with unlimited growth X meaning 1/x will decrease and approach zero.
As you can see, to solve the limit, you just need to substitute the value to strive for into the function X . However, this is the simplest case. Often finding the limit is not so obvious. Within the limits there are uncertainties of the type 0/0 or infinity/infinity . What to do in such cases? Resort to tricks!
Uncertainties within
Uncertainty of the form infinity/infinity
Let there be a limit:
If we try to substitute infinity into the function, we will get infinity in both the numerator and the denominator. In general, it is worth saying that there is a certain element of art in resolving such uncertainties: you need to notice how you can transform the function in such a way that the uncertainty goes away. In our case, we divide the numerator and denominator by X in the senior degree. What will happen?
From the example already discussed above, we know that terms containing x in the denominator will tend to zero. Then the solution to the limit is:
To resolve type uncertainties infinity/infinity divide the numerator and denominator by X to the highest degree.
By the way! For our readers there is now a 10% discount on any type of work
Another type of uncertainty: 0/0
As always, substituting values into the function x=-1 gives 0 in the numerator and denominator. Look a little more closely and you will notice that we have a quadratic equation in the numerator. Let's find the roots and write:
Let's reduce and get:
So, if you are faced with type uncertainty 0/0 – factor the numerator and denominator.
To make it easier for you to solve examples, we present a table with the limits of some functions:
L'Hopital's rule within
Another powerful way, allowing to eliminate uncertainties of both types. What is the essence of the method?
If there is uncertainty in the limit, take the derivative of the numerator and denominator until the uncertainty disappears.
L'Hopital's rule looks like this:
Important point : the limit in which the derivatives of the numerator and denominator stand instead of the numerator and denominator must exist.
And now - a real example:
There is typical uncertainty 0/0 . Let's take the derivatives of the numerator and denominator:
Voila, uncertainty is resolved quickly and elegantly.
We hope that you will be able to usefully apply this information in practice and find the answer to the question “how to solve limits in higher mathematics.” If you need to calculate the limit of a sequence or the limit of a function at a point, but there is absolutely no time for this work, contact a professional student service for a quick and detailed solution.
