www.siteيسمح لك بالعثور على ملفات . يقوم الموقع بالحساب. في غضون ثوانٍ قليلة، سيقدم الخادم الحل الصحيح. المعادلة المميزة للمصفوفةسيكون تعبيرًا جبريًا تم العثور عليه باستخدام قاعدة حساب المحدد المصفوفات المصفوفاتبينما على طول القطر الرئيسي سيكون هناك اختلافات في قيم العناصر القطرية والمتغير. عند الحساب المعادلة المميزة للمصفوفة على الانترنت، كل عنصر المصفوفاتسيتم ضربها مع العناصر الأخرى المقابلة المصفوفات. البحث في الوضع متصلممكن فقط للمربع المصفوفات. عملية البحث المعادلة المميزة للمصفوفة على الانترنتيقلل من حساب المجموع الجبري لمنتج العناصر المصفوفاتنتيجة لإيجاد المحدد المصفوفات، فقط لغرض التحديد المعادلة المميزة للمصفوفة على الانترنت. وتحتل هذه العملية مكانة خاصة في النظرية المصفوفات، يسمح لك بالعثور على القيم الذاتية والمتجهات باستخدام الجذور. مهمة العثور المعادلة المميزة للمصفوفة على الانترنتيتكون من عناصر مضاعفة المصفوفاتمتبوعًا بجمع هذه المنتجات وفقًا لقاعدة معينة. www.siteيجد المعادلة المميزة للمصفوفةالبعد المحدد في الوضع متصل. حساب المعادلة المميزة للمصفوفة على الانترنتنظرا لبعدها، فهذا هو إيجاد كثيرة الحدود ذات معاملات عددية أو رمزية، وجدت وفقا لقاعدة حساب المحدد المصفوفات- كمجموع منتجات العناصر المقابلة المصفوفات، فقط لغرض التحديد المعادلة المميزة للمصفوفة على الانترنت. العثور على كثيرة الحدود فيما يتعلق بمتغير للمعادلة التربيعية المصفوفات، كتعريف المعادلة المميزة للمصفوفة، شائع من الناحية النظرية المصفوفات. معنى جذور كثير الحدود المعادلة المميزة للمصفوفة على الانترنتتستخدم لتحديد المتجهات الذاتية والقيم الذاتية لـ المصفوفات. علاوة على ذلك، إذا كان المحدد المصفوفاتسوف يساوي الصفر، الذي - التي المعادلة المميزة للمصفوفةسيظل موجودا، على عكس العكس المصفوفات. من أجل الحساب المعادلة المميزة للمصفوفةأو البحث عن عدة في وقت واحد مصفوفات المعادلات المميزة، تحتاج إلى قضاء الكثير من الوقت والجهد، بينما سيجد خادمنا ذلك في غضون ثوانٍ المعادلة المميزة للمصفوفة على الانترنت. في هذه الحالة الجواب على إيجاد المعادلة المميزة للمصفوفة على الانترنتسوف تكون صحيحة وبدقة كافية، حتى لو كانت الأرقام عند العثور عليها المعادلة المميزة للمصفوفة على الانترنتسيكون غير عقلاني. على الموقع www.siteيُسمح بإدخالات الأحرف في العناصر المصفوفات، إنه المعادلة المميزة للمصفوفة على الانترنتيمكن تمثيلها بشكل رمزي عام عند الحساب المعادلة المميزة للمصفوفة على الانترنت. من المفيد التحقق من الإجابة التي تم الحصول عليها عند حل مشكلة البحث المعادلة المميزة للمصفوفة على الانترنتباستخدام الموقع www.site. عند إجراء عملية حساب كثير الحدود - المعادلة المميزة للمصفوفة، عليك أن تكون حذرًا ومركزًا للغاية عند حل هذه المشكلة. بدوره، سيساعدك موقعنا على التحقق من قرارك بشأن الموضوع المعادلة المميزة للمصفوفة على الانترنت. إذا لم يكن لديك الوقت لإجراء فحوصات طويلة للمشكلات التي تم حلها، إذن www.siteستكون بالتأكيد أداة ملائمة للتحقق عند البحث والحساب المعادلة المميزة للمصفوفة على الانترنت.

تعليمات

يُطلق على الرقم k قيمة ذاتية (رقم) للمصفوفة A إذا كان هناك متجه x بحيث يكون Ax=kx. (1) في هذه الحالة، يسمى المتجه x بالمتجه الذاتي للمصفوفة A، الموافق للرقم k. في الفضاء R^n (انظر الشكل 1)، يكون للمصفوفة A الشكل كما في الشكل.

من الضروري تحديد مهمة العثور على متجهات المصفوفة A. دع المتجه الذاتي x يُعطى بواسطة الإحداثيات. في شكل مصفوفة، سيتم كتابتها كمصفوفة عمود، والتي ينبغي تمثيلها كصف منقول للراحة. X=(x1,x2,…,xn)^T. بناءً على (1)، Ax-khx=0 أو Ax-kEx=0، حيث E هي مصفوفة الهوية (العناصر الموجودة على القطر الرئيسي، وجميع العناصر الأخرى هي أصفار ). ثم (A-kE)x=0. (2)

التعبير (2) للمعادلات الجبرية المتجانسة الخطية له حل غير صفري (متجه ذاتي). ولذلك فإن المحدد الرئيسي للنظام (2) يساوي الصفر، أي |A-kE|=0. (3) تسمى المساواة الأخيرة للقيمة الذاتية k بالمعادلة المميزة للمصفوفة A ولها الشكل الموسع (انظر الشكل 2).

استبدال الجذر k للمعادلة المميزة في النظام (2)، وهو نظام متجانس من المعادلات الخطية بمصفوفة فردية (محددها هو صفر). كل حل غير صفري لهذا النظام هو ناقل ذاتي للمصفوفة A يتوافق مع قيمة ذاتية معينة k (أي جذر المعادلة المميزة).

مثال. أوجد القيم الذاتية ومتجهات المصفوفة A (انظر الشكل 3). يتم عرض المعادلة المميزة في الشكل. 3. قم بتوسيع المحدد وابحث عن القيم الذاتية للمصفوفة، وهي المعادلة المعطاة (3-k)(-1-k)-5=0، (k-3)(k+1)-5=0 ، k^2-2k -8=0 جذورها هي k1=4، k2=-2

أ) تم العثور على المتجهات الذاتية المقابلة لـ k1=4 عن طريق حل النظام (A-4kE)x=0. في هذه الحالة، مطلوب معادلات واحدة فقط، حيث من الواضح أن محدد النظام يساوي الصفر. إذا وضعنا x=(x1, x2)^T، فإن المعادلة الأولى للنظام هي (1-4)x1+x2=0, -3x1+x2=0. إذا افترضنا أن x1=1 (ولكن ليس الصفر)، فإن x2=3. نظرًا لأن النظام المتجانس ذو المصفوفة المفردة يحتوي على العديد من الحلول غير الصفرية حسب الرغبة، فإن المجموعة الكاملة من المتجهات الذاتية المقابلة للقيمة الذاتية الأولى x =C1(1, 3), C1=const.

ب) أوجد المتجهات الذاتية المقابلة لـ k2=-2. عند حل النظام (A+2kE)x=0 فإن معادلته الأولى هي (3+2)x1+x2=0، 5x1+x2=0 إذا وضعنا x1=1، فإن x2=-5. المتجهات الذاتية المقابلة x =C2(1, 3), C2=const. المجموعة الإجمالية لجميع المتجهات الذاتية لمصفوفة معينة: x = C1(1, 3)+ C2(1, 3).

مصادر:

• بيسكونوف إن إس. حساب التفاضل والتكامل. م، 1976، - 576 ص.
• العثور على القيم الذاتية ومتجهات المصفوفة

تُستخدم المصفوفات، وهي شكل جدولي لتسجيل البيانات، على نطاق واسع عند العمل مع أنظمة المعادلات الخطية. علاوة على ذلك، فإن عدد المعادلات يحدد عدد صفوف المصفوفة، وعدد المتغيرات يحدد ترتيب أعمدتها. ونتيجة لذلك، يتم تقليل حل الأنظمة الخطية إلى العمليات على المصفوفات، وأحدها هو إيجاد القيم الذاتية للمصفوفة. يتم حسابها باستخدام المعادلة المميزة. يمكن تعريف القيم الذاتية لمصفوفة مربعة من الرتبة m.

تعليمات

اكتب مربعًا معينًا A. للعثور على قيمه الذاتية، استخدم المعادلة المميزة الناتجة عن شرط الحل غير البديهي لنظام متجانس خطي، ممثلًا في هذه الحالة بمصفوفة مربعة. كما يلي من كريمر، يوجد الحل فقط إذا كان محدده يساوي الصفر. وبذلك يمكننا كتابة المعادلة | أ -  | = 0، حيث A هي القيمة المعطاة، α هي الأرقام المطلوبة، E هي مصفوفة الهوية التي تكون فيها جميع العناصر الموجودة على القطر الرئيسي تساوي واحدًا، والباقي يساوي صفرًا.

اضرب المتغير المطلوب lect بمصفوفة الهوية E التي لها نفس البعد الأصلي المعطى A. وستكون نتيجة العملية مصفوفة حيث تقع قيم lect على طول القطر الرئيسي، وتبقى العناصر المتبقية مساوية للصفر .

المصفوفات القطرية لها أبسط بنية. السؤال الذي يطرح نفسه هو ما إذا كان من الممكن العثور على الأساس الذي المصفوفة المشغل الخطيسيكون لها مظهر قطري. مثل هذا الأساس موجود.
دعونا نعطي مساحة خطية R n وعامل خطي A يعمل فيها؛ في هذه الحالة، المشغل A يأخذ R n إلى نفسه، أي A:R n → R n .

تعريف. يسمى المتجه غير الصفري x بالمتجه الذاتي للعامل A إذا قام العامل A بتحويل x إلى متجه خطي متداخل، أي. يُطلق على الرقم lect القيمة الذاتية أو القيمة الذاتية للمشغل A، وهو ما يتوافق مع المتجه الذاتي x.
دعونا نلاحظ بعض خصائص القيم الذاتية والمتجهات الذاتية.
1. أي مجموعة خطية من المتجهات الذاتية المشغل A المطابق لنفس القيمة الذاتية π هو ناقل ذاتي له نفس القيمة الذاتية.
2. المتجهات الذاتية المشغل A ذو القيم الذاتية المختلفة الزوجية π 1 , π 2 , ..., π m مستقلة خطيا.
3. إذا كانت القيم الذاتية 1 = 2 = 1 م = 1، فإن القيمة الذاتية 5 لا تتوافق مع أكثر من م من المتجهات الذاتية المستقلة خطيًا.

لذا، إذا كان هناك n متجهات ذاتية مستقلة خطيًا ، المقابلة لقيم ذاتية مختلفة ​​1، 1، 2، ...، 5 n، فهي مستقلة خطيًا، لذلك يمكن اعتبارها أساسًا للمساحة R n. دعونا نجد شكل مصفوفة العامل الخطي A على أساس ناقلاته الذاتية، والتي سنتعامل معها مع العامل A على أساس المتجهات: ثم .
وبالتالي، فإن مصفوفة العامل الخطي A في أساس ناقلاته الذاتية لها شكل قطري، وتكون القيم الذاتية للعامل A على طول القطر.
هل هناك أساس آخر تكون فيه المصفوفة ذات شكل قطري؟ الجواب على هذا السؤال يتم تقديمه من خلال النظرية التالية.

نظرية. مصفوفة العامل الخطي A في الأساس (i = 1..n) لها شكل قطري إذا وفقط إذا كانت جميع متجهات الأساس هي متجهات ذاتية للعامل A.

قاعدة إيجاد القيم الذاتية والمتجهات الذاتية

دعونا نعطي المتجه ، حيث x 1 , x 2 , …, x n هي إحداثيات المتجه x بالنسبة إلى الأساس و x هو المتجه الذاتي للعامل الخطي A المطابق للقيمة الذاتية π، أي. يمكن كتابة هذه العلاقة على شكل مصفوفة

. (*)

يمكن اعتبار المعادلة (*) معادلة لإيجاد x، أي أننا مهتمون بالحلول غير التافهة، حيث لا يمكن أن يكون المتجه الذاتي صفراً. من المعروف أن الحلول غير البديهية لنظام متجانس من المعادلات الخطية موجودة إذا وفقط إذا كانت det(A - lectE) = 0. وبالتالي، لكي تكون lect قيمة ذاتية للعامل A فمن الضروري والكافي أن يكون det(A - lectE) ) = 0.
إذا كتبت المعادلة (*) بالتفصيل بالشكل الإحداثي، نحصل على نظام من المعادلات الخطية المتجانسة:

(1)
أين - مصفوفة المشغل الخطية.

النظام (1) له حل غير صفري إذا كان محدده D يساوي الصفر

لقد حصلنا على معادلة لإيجاد القيم الذاتية.
تسمى هذه المعادلة المعادلة المميزة، ويسمى جانبها الأيسر متعدد الحدود المميز للمصفوفة (المشغل) A. إذا لم يكن لمتعدد الحدود المميز جذور حقيقية، فإن المصفوفة A لا تحتوي على متجهات ذاتية ولا يمكن اختزالها إلى شكل قطري.
لتكن lect 1, lect 2, …, lect n هي الجذور الحقيقية للمعادلة المميزة، ومن الممكن أن يكون هناك مضاعفات بينها. باستبدال هذه القيم بدورها في النظام (1)، نجد المتجهات الذاتية.

مثال 12. العامل الخطي A يعمل في R 3 وفقًا للقانون، حيث x 1, x 2, .., x n هي إحداثيات المتجه في الأساس , , . ابحث عن القيم الذاتية والمتجهات الذاتية لهذا العامل.
حل. نحن نبني مصفوفة هذا العامل:
.
نقوم بإنشاء نظام لتحديد إحداثيات المتجهات الذاتية:

نؤلف معادلة مميزة ونحلها:

.
 1,2 = -1،  3 = 3.
بالتعويض بـ lect = -1 في النظام نحصل على:
أو
لأن ، ثم هناك متغيران تابعان ومتغير حر واحد.
دع x 1 يكون مجهولًا حرًا، إذن نحل هذا النظام بأي طريقة ونجد الحل العام لهذا النظام: النظام الأساسي للحلول يتكون من حل واحد، حيث أن n - r = 3 - 2 = 1.
مجموعة المتجهات الذاتية المقابلة للقيمة الذاتية lect = -1 لها الشكل: حيث x 1 هو أي رقم غير الصفر. لنختار متجهًا واحدًا من هذه المجموعة، على سبيل المثال، نضع x 1 = 1: .
بالاستدلال بالمثل، نجد المتجهات الذاتية المقابلة للقيمة الذاتية 3 = 3: .
في الفضاء R 3، يتكون الأساس من ثلاثة متجهات مستقلة خطيًا، لكننا تلقينا فقط اثنين من المتجهات الذاتية المستقلة خطيًا، والتي لا يمكن تكوين الأساس في R 3 منها. وبالتالي، لا يمكننا تقليل المصفوفة A للعامل الخطي إلى الشكل القطري.

مثال 13. نظرا للمصفوفة .
1. إثبات أن الناقل هو متجه ذاتي للمصفوفة A. أوجد القيمة الذاتية المقابلة لهذا المتجه الذاتي.
2. أوجد أساسًا تكون فيه المصفوفة A ذات شكل قطري.
حل.
1. إذا كان x هو متجه ذاتي

.
المتجه (1، 8، -1) هو متجه ذاتي. القيمة الذاتية π = -1.
المصفوفة لها شكل قطري في أساس يتكون من ناقلات ذاتية. واحد منهم مشهور. دعونا نجد الباقي.
نحن نبحث عن المتجهات الذاتية من النظام:

المعادلة المميزة: ;
(3 + )[-2(2-)(2+)+3] = 0; (3+)( 2 - 1) = 0
lect 1 = -3، lect 2 = 1، lect 3 = -1.
لنجد المتجه الذاتي المطابق للقيمة الذاتية π = -3:

رتبة مصفوفة هذا النظام هي اثنان وتساوي عدد المجهولين، لذلك هذا النظام لديه حل صفري فقط x 1 = x 3 = 0. x 2 هنا يمكن أن يكون أي شيء آخر غير الصفر، على سبيل المثال، x 2 = 1. وبالتالي، فإن المتجه (0،1،0) هو ناقل ذاتي يقابل α = -3. دعونا نتحقق:
.
إذا كانت 1 = 1، نحصل على النظام
رتبة المصفوفة اثنان. نحذف المعادلة الأخيرة.
دع x 3 يكون مجهولًا مجانيًا. إذن x 1 = -3x 3، 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3، x 2 = -9x 3.
بافتراض أن x 3 = 1، لدينا (-3،-9،1) - ناقل ذاتي يتوافق مع القيمة الذاتية 1 = 1. تحقق مما يلي:

.
نظرًا لأن القيم الذاتية حقيقية ومتميزة، فإن المتجهات المقابلة لها تكون مستقلة خطيًا، لذا يمكن أخذها كأساس في R 3 . وهكذا في الأساس , , المصفوفة A لها الشكل:
.
لا يمكن اختزال كل مصفوفة للمشغل الخطي A:R n → R n إلى شكل قطري، لأنه بالنسبة لبعض العوامل الخطية قد يكون هناك أقل من n من المتجهات الذاتية المستقلة الخطية. ومع ذلك، إذا كانت المصفوفة متماثلة، فإن جذر المعادلة المميزة للتعددية m يتوافق مع المتجهات المستقلة خطيًا تمامًا.

تعريف. المصفوفة المتماثلة هي مصفوفة مربعة تكون فيها العناصر المتماثلة حول القطر الرئيسي متساوية، أي فيها.
ملحوظات. 1. جميع القيم الذاتية للمصفوفة المتماثلة حقيقية.
2. إن المتجهات الذاتية للمصفوفة المتماثلة المقابلة للقيم الذاتية المختلفة الزوجية تكون متعامدة.
وكأحد التطبيقات العديدة للجهاز المدروس، فإننا نعتبر مشكلة تحديد نوع منحنى الدرجة الثانية.

"يحدد الجزء الأول الأحكام الضرورية إلى الحد الأدنى لفهم القياسات الكيميائية، ويحتوي الجزء الثاني على الحقائق التي تحتاج إلى معرفتها لفهم أعمق لأساليب التحليل متعدد المتغيرات. تم توضيح العرض التقديمي باستخدام الأمثلة الواردة في مصنف Excel Matrix.xls، والتي تصاحب هذه الوثيقة.

يتم وضع روابط الأمثلة في النص ككائنات Excel. هذه الأمثلة مجردة بطبيعتها، ولا ترتبط بأي حال من الأحوال بمشاكل الكيمياء التحليلية. تمت مناقشة أمثلة واقعية لاستخدام جبر المصفوفة في القياسات الكيميائية في نصوص أخرى تغطي مجموعة متنوعة من تطبيقات القياس الكيميائي.

معظم القياسات التي يتم إجراؤها في الكيمياء التحليلية ليست مباشرة، ولكن غير مباشر. وهذا يعني أنه في التجربة، بدلاً من قيمة المادة التحليلية المطلوبة C (التركيز)، يتم الحصول على قيمة أخرى س(إشارة)، مرتبطة بـ C ولكنها لا تساويها، أي. س(ج) ≠ ج. كقاعدة عامة، نوع الاعتماد س(C) غير معروف، ولكن لحسن الحظ في الكيمياء التحليلية تكون معظم القياسات متناسبة. وهذا يعني أنه مع زيادة تركيز C في أمرات، إشارة X سوف تزيد بنفس المقدار، أي. س(أج) = س(ج). بالإضافة إلى ذلك، تكون الإشارات أيضًا إضافية، وبالتالي فإن الإشارة من العينة التي تحتوي على مادتين بتركيزات C 1 وC 2 ستكون مساوية لمجموع الإشارات من كل مكون، أي. س(ج1 + ج2) = س(ج1)+ س(ج2). التناسب والإضافة معا يعطيان الخطية. ويمكن إعطاء أمثلة كثيرة لتوضيح مبدأ الخطية، ولكن يكفي أن نذكر المثالين الأكثر وضوحا - اللوني والتحليل الطيفي. الميزة الثانية المتأصلة في تجربة الكيمياء التحليلية هي متعدد القنوات. تقوم المعدات التحليلية الحديثة بقياس الإشارات للعديد من القنوات في نفس الوقت. على سبيل المثال، يتم قياس شدة انتقال الضوء لعدة أطوال موجية في وقت واحد، أي. نطاق. لذلك، في التجربة نتعامل مع العديد من الإشارات س 1 , س 2 ,...., س n، التي تميز مجموعة التركيزات C 1 , C 2 , ..., C m من المواد الموجودة في النظام قيد الدراسة.

أرز. 1 أطياف

لذلك، تتميز التجربة التحليلية بالخطية وتعدد الأبعاد. ولذلك، فمن الملائم اعتبار البيانات التجريبية كمتجهات ومصفوفات ومعالجتها باستخدام جهاز جبر المصفوفات. يتم توضيح جدوى هذا النهج من خلال المثال الموضح في، والذي يعرض ثلاثة أطياف مأخوذة عند 200 طول موجي من 4000 إلى 4796 سم −1. أولاً ( س 1) والثانية ( س 2) تم الحصول على الأطياف للعينات القياسية التي يُعرف فيها تركيز مادتين A وB: في العينة الأولى [A] = 0.5، [B] = 0.1، وفي العينة الثانية [A] = 0.2، [ ب] = 0.6. ماذا يمكن أن يقال عن عينة جديدة غير معروفة يشار إلى طيفها س 3 ?

دعونا نفكر في ثلاثة أطياف تجريبية س 1 , س 2 و س 3 كثلاثة متجهات للبعد 200. باستخدام الجبر الخطي، يمكن للمرء بسهولة إظهار ذلك س 3 = 0.1 س 1 +0.3 س 2، لذلك من الواضح أن العينة الثالثة تحتوي فقط على المادتين A وB بتركيزات [A] = 0.5×0.1 + 0.2×0.3 = 0.11 و[B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. المعلومات الأساسية

1.1 المصفوفات

مصفوفةيسمى جدول مستطيل من الأرقام، على سبيل المثال

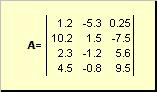
أرز. 2 مصفوفة

يتم الإشارة إلى المصفوفات بأحرف كبيرة وعريضة ( أ)، وعناصرها - من خلال الحروف الصغيرة المقابلة للمؤشرات، أي. أأنا. الفهرس الأول يقوم بترقيم الصفوف، والثاني - الأعمدة. في القياس الكيميائي، من المعتاد الإشارة إلى القيمة القصوى للمؤشر بنفس حرف المؤشر نفسه، ولكن بأحرف كبيرة. لذلك المصفوفة أيمكن كتابتها أيضًا كـ ( أ أنا , أنا = 1,..., أنا; ي = 1,..., ج). بالنسبة لمصفوفة المثال أنا = 4, ج= 3 و أ 23 = −7.5.

زوج من الأرقام أناو جيسمى البعد المصفوفة ويشار إليه باسم أنا× ج. مثال على المصفوفة في القياسات الكيميائية هو مجموعة من الأطياف التي تم الحصول عليها أناعينات ل جالأطوال الموجية.

1.2. أبسط العمليات على المصفوفات

يمكن أن تكون المصفوفات اضرب بالأرقام. في هذه الحالة، يتم ضرب كل عنصر بهذا الرقم. على سبيل المثال -

أرز. 3 ضرب المصفوفة بعدد

يمكن أن تكون مصفوفتان لهما نفس البعد عنصرًا بعنصر طيةو طرح. على سبيل المثال،

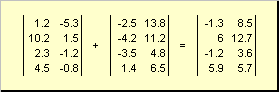
أرز. 4 إضافة مصفوفة

نتيجة الضرب بعدد والجمع يتم الحصول على مصفوفة من نفس البعد.

المصفوفة الصفرية هي مصفوفة تتكون من أصفار. تم تعيينه يا. من الواضح أن أ+يا = أ, أ−أ = ياو 0 أ = يا.

يمكن أن تكون المصفوفة تبديل. خلال هذه العملية، يتم قلب المصفوفة، أي. يتم تبديل الصفوف والأعمدة. تتم الإشارة إلى النقل بواسطة أولية ، أ"أو الفهرس أر. وهكذا إذا أ = {أ أنا , أنا = 1,..., أنا; ي = 1,...,ج)، الذي - التي أر = ( أ جي , ي = 1,...,ج; ط = 1،...، أنا). على سبيل المثال

أرز. 5 تبديل المصفوفة

ومن الواضح أن ( أر) ر = أ, (أ+ب) ر = أر+ بر.

1.3. ضرب المصفوفة

يمكن أن تكون المصفوفات ضاعفولكن فقط إذا كانت ذات أبعاد مناسبة. لماذا هذا سوف يكون واضحا من التعريف. منتج المصفوفة أالبعد أنا× ك، والمصفوفات بالبعد ك× ج، تسمى مصفوفة جالبعد أنا× ج، وعناصرها عبارة عن أرقام

وهكذا بالنسبة للمنتج أ.بفمن الضروري أن عدد الأعمدة في المصفوفة اليسرى أكان يساوي عدد الصفوف في المصفوفة اليمنى ب. مثال على منتج المصفوفة -

الشكل 6: منتج المصفوفات

يمكن صياغة قاعدة ضرب المصفوفات على النحو التالي. للعثور على عنصر المصفوفة ج، واقفاً عند التقاطع أنا- السطر و يالعمود العاشر ( ج أنا) يجب ضرب عنصر بعنصر أنا-الصف من المصفوفة الأولى أعلى يالعمود الرابع من المصفوفة الثانية بوجمع كل النتائج. لذلك في المثال الموضح، يتم الحصول على عنصر من الصف الثالث والعمود الثاني كمجموع منتجات الصف الثالث من حيث العناصر أوالعمود الثاني ب

الشكل 7: عنصر منتج المصفوفات

يعتمد منتج المصفوفات على الترتيب، أي. أ.ب ≠ بكالوريوس.، على الأقل لأسباب الأبعاد. يقولون أنه غير تبادلي. ومع ذلك، فإن منتج المصفوفات هو ترابطي. وهذا يعني ذلك اي بي سي = (أ.ب)ج = أ(قبل الميلاد). بالإضافة إلى ذلك، فهي أيضًا توزيعية، أي. أ(ب+ج) = أ.ب+مكيف الهواء. من الواضح أن أ.و. = يا.

1.4. المصفوفات المربعة

إذا كان عدد أعمدة المصفوفة يساوي عدد صفوفها ( أنا = ي = ن)، فإن هذه المصفوفة تسمى مربع. في هذا القسم سننظر فقط في هذه المصفوفات. ومن بين هذه المصفوفات يمكن تمييز المصفوفات ذات الخصائص الخاصة.

أعزبمصفوفة (المشار إليها أنا،وأحيانا ه) هي مصفوفة تكون جميع عناصرها مساوية للصفر، باستثناء العناصر القطرية التي تساوي 1، أي.

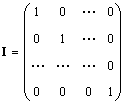
بوضوح منظمة العفو الدولية. = أ. = أ.

المصفوفة تسمى قطري، إذا كانت جميع عناصره باستثناء العناصر القطرية ( أ ثانيا) تساوي الصفر. على سبيل المثال

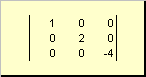
أرز. 8 مصفوفة قطرية

مصفوفة أدعا الأعلى الثلاثي، إذا كانت جميع عناصره الواقعة تحت القطر تساوي الصفر، أي. أ أنا= 0، في أنا>ي. على سبيل المثال

أرز. 9 المصفوفة الثلاثية العليا

يتم تعريف المصفوفة المثلثية السفلية بالمثل.

مصفوفة أمُسَمًّى متماثل، لو أر = أ. بعبارة أخرى أ أنا = أ جي. على سبيل المثال

أرز. 10 مصفوفة متماثلة

مصفوفة أمُسَمًّى متعامد، لو

أر أ = أ.أ.ر = أنا.

المصفوفة تسمى طبيعيلو

1.5. التتبع والمحدد

التاليمصفوفة مربعة أ(يُشار إليه بواسطة Tr( أ) أو س( أ)) هو مجموع عناصره القطرية،

على سبيل المثال،

أرز. 11 تتبع المصفوفة

من الواضح أن

س (α أ) = α س( أ) و

س ( أ+ب) = س( أ)+ س( ب).

يمكن أن يظهر ذلك

س ( أ) = س( أر)، س ( أنا) = ن,

وأيضا ذلك

س ( أ.ب) = س( بكالوريوس.).

سمة أخرى مهمة للمصفوفة المربعة هي المحدد(يشار إليه بـ( أ)). تحديد المحدد في الحالة العامة أمر صعب للغاية، لذلك سنبدأ بالخيار الأبسط - المصفوفة أالبعد (2×2). ثم

بالنسبة للمصفوفة (3×3)، فإن المحدد سيكون مساويًا لـ

في حالة المصفوفة ( ن× ن) يتم حساب المحدد كمجموع 1·2·3· ... · ن= ن! حيث أن كل منها متساوي

الفهارس ك 1 , ك 2 ,..., ك نيتم تعريفها على أنها جميع التباديلات المرتبة الممكنة صالأرقام في المجموعة (1، 2، ...، ن). يعد حساب محدد المصفوفة إجراءً معقدًا يتم تنفيذه عمليًا باستخدام برامج خاصة. على سبيل المثال،

أرز. 12 محدد المصفوفة

دعونا نلاحظ فقط الخصائص الواضحة:

ديت ( أنا) = 1، ديت ( أ) = ديت( أر)،

ديت ( أ.ب) = ديت( أ)حذف( ب).

1.6. المتجهات

إذا كانت المصفوفة تتكون من عمود واحد فقط ( ج= 1)، ثم يتم استدعاء مثل هذا الكائن ناقلات. بتعبير أدق، ناقل العمود. على سبيل المثال

يمكن للمرء أيضًا اعتبار المصفوفات التي تتكون من صف واحد، على سبيل المثال

هذا الكائن هو أيضًا ناقل، ولكن ناقلات الصف. عند تحليل البيانات، من المهم أن نفهم المتجهات التي نتعامل معها - الأعمدة أو الصفوف. لذلك يمكن اعتبار الطيف المأخوذ لعينة واحدة بمثابة متجه صف. ثم ينبغي التعامل مع مجموعة الكثافات الطيفية عند طول موجي معين لجميع العينات على أنها متجه عمود.

البعد المتجه هو عدد عناصره.

من الواضح أنه يمكن تحويل أي متجه عمود إلى متجه صف عن طريق التبديل، أي.

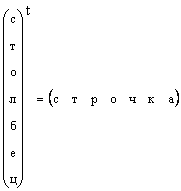
في الحالات التي لم يتم فيها تحديد شكل المتجه بشكل محدد، ولكن يُقال ببساطة أنه متجه، فإن ذلك يعني متجه عمود. سوف نلتزم أيضًا بهذه القاعدة. تتم الإشارة إلى المتجه بحرف صغير ومستقيم وعريض. المتجه الصفري هو متجه جميع عناصره صفر. تم تعيينه 0 .

1.7. أبسط العمليات مع المتجهات

يمكن جمع المتجهات وضربها بالأرقام بنفس طريقة المصفوفات. على سبيل المثال،

أرز. 13 العمليات مع المتجهات

اثنين من المتجهات سو ذيتم استدعاؤها خطي، إذا كان هناك رقم α هكذا

1.8. منتجات المتجهات

متجهان من نفس البعد نيمكن أن تتضاعف. يجب أن يكون هناك ناقلان س = (س 1 , س 2 ,...,سن)ر و ذ = (ذ 1 , ذ 2 ,...,ذن) ر . مسترشدين بقاعدة الضرب صفًا بعمود، يمكننا تكوين منتجين منهما: سر ذو xyر. العمل الأول

مُسَمًّى العدديةأو داخلي. نتيجته رقم. ويشار إليه أيضًا بـ ( س,ذ)= سر ذ. على سبيل المثال،

أرز. 14 المنتج الداخلي (العددي).

القطعة الثانية

مُسَمًّى خارجي. والنتيجة هي مصفوفة البعد ( ن× ن). على سبيل المثال،

أرز. 15 عمل خارجي

تسمى المتجهات التي يكون حاصل ضربها القياسي صفرًا متعامد.

1.9. قاعدة المتجهات

يُطلق على المنتج العددي للمتجه مع نفسه اسم المربع العددي. هذه القيمة

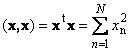
يحدد مربع طولناقلات س. للإشارة إلى الطول (ويسمى أيضًا القاعدةالمتجه) يتم استخدام الترميز

على سبيل المثال،

أرز. 16 قاعدة المتجهات

متجه طول الوحدة (|| س|| = 1) يسمى تطبيع. ناقل غير صفري ( س ≠ 0 ) يمكن تطبيعها بتقسيمها على الطول، أي. س = ||س|| (س/||س||) = ||س|| ه. هنا ه = س/||س|| - ناقلات تطبيع.

تسمى المتجهات متعامدة إذا كانت جميعها طبيعية ومتعامدة بشكل زوجي.

1.10. الزاوية بين المتجهات

المنتج العددي يحدد و ركنφ بين ناقلين سو ذ

إذا كانت المتجهات متعامدة، فإن cosφ = 0 و φ = π/2، وإذا كانت على خط مستقيم، فإن cosφ = 1 و φ = 0.

1.11. تمثيل المتجهات للمصفوفة

كل مصفوفة أمقاس أنا× جيمكن تمثيلها كمجموعة من المتجهات

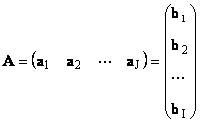
هنا كل ناقلات أ ييكون يالعمود العاشر ومتجه الصف ب أنايكون أناالصف العاشر من المصفوفة أ

1.12. المتجهات المعتمدة خطياً

ناقلات من نفس البعد ( ن) يمكن جمعها وضربها برقم، تمامًا مثل المصفوفات. ستكون النتيجة متجهًا بنفس البعد. يجب أن يكون هناك عدة نواقل لها نفس البعد س 1 , س 2 ,...,س K ونفس عدد الأرقام α α 1 , α 2 ,...,α ك. ناقل

ذ= α 1 س 1 + ألفا 2 س 2 +...+ أ ك س ك

مُسَمًّى مزيج خطيناقلات س ك .

إذا كان هناك مثل هذه الأرقام غير الصفرية α ك ≠ 0, ك = 1,..., ك، ماذا ذ = 0 ، ثم هذه المجموعة من المتجهات س كمُسَمًّى تعتمد خطيا. وبخلاف ذلك، يقال إن المتجهات مستقلة خطيًا. على سبيل المثال، المتجهات س 1 = (2، 2)ر و س 2 = (−1, −1) t يعتمدان خطيًا، لأن س 1 +2س 2 = 0

1.13. رتبة المصفوفة

النظر في مجموعة من كناقلات س 1 , س 2 ,...,س كأبعاد ن. رتبة هذا النظام من المتجهات هي الحد الأقصى لعدد المتجهات المستقلة خطيًا. على سبيل المثال في المجموعة

على سبيل المثال، لا يوجد سوى متجهين مستقلين خطيا س 1 و س 2، لذا فإن رتبته هي 2.

من الواضح أنه إذا كان عدد المتجهات في المجموعة أكبر من أبعادها ( ك>ن)، فإنهم بالضرورة يعتمدون خطيًا.

رتبة المصفوفة(يشار إليه بالرتبة( أ)) هي رتبة نظام المتجهات الذي يتكون منه. على الرغم من أنه يمكن تمثيل أي مصفوفة بطريقتين (متجهات الأعمدة أو الصفوف)، إلا أن هذا لا يؤثر على قيمة الترتيب، لأن

1.14. مصفوفة معكوسة

مصفوفة مربعة أويسمى غير منحط إذا كان له فريدة يعكسمصفوفة أ-1، تحددها الشروط

أ.أ. −1 = أ −1 أ = أنا.

المصفوفة العكسية غير موجودة في جميع المصفوفات. الشرط الضروري والكافي لعدم الانحطاط هو

ديت ( أ) ≠ 0 أو الرتبة( أ) = ن.

يعد انعكاس المصفوفة إجراءً معقدًا توجد به برامج خاصة. على سبيل المثال،

أرز. 17 انعكاس المصفوفة

دعونا نقدم الصيغ لأبسط حالة - مصفوفة 2 × 2

إذا المصفوفات أو بفهي غير منحطة، ثم

(أ.ب) −1 = ب −1 أ −1 .

1.15. مصفوفة عكسية زائفة

إذا مصفوفة أمفرد والمصفوفة العكسية غير موجودة، وفي بعض الحالات يمكنك استخدامها معكوس زائفالمصفوفة، والتي يتم تعريفها على أنها مصفوفة أ+ ذلك

أ.أ. + أ = أ.

المصفوفة العكسية الكاذبة ليست الوحيدة ويعتمد شكلها على طريقة بنائها. على سبيل المثال، بالنسبة للمصفوفة المستطيلة، يمكنك استخدام طريقة مور-بنروز.

إذا كان عدد الأعمدة أقل من عدد الصفوف

أ + =(أر أ) −1 أر

على سبيل المثال،

أرز. 17a الانقلاب الزائف للمصفوفة

إذا كان عدد الأعمدة أكبر من عدد الصفوف

أ + =أر( أ.أ.ر) −1

1.16. ضرب المتجه بمصفوفة

ناقل سيمكن ضربها بمصفوفة أحجم مناسب. في هذه الحالة، يتم ضرب متجه العمود على اليمين الفأس، والصف المتجه على اليسار سر أ. إذا كان البعد ناقلات ج، والبعد المصفوفة أنا× جفإن النتيجة ستكون متجه البعد أنا. على سبيل المثال،

أرز. 18 ضرب المتجه بمصفوفة

إذا مصفوفة أ- مربع ( أنا× أنا)، ثم المتجه ذ = الفأسله نفس البعد س. من الواضح أن

أ(ألفا 1 س 1 + ألفا 2 س 2) = α 1 الفأس 1 + ألفا 2 الفأس 2 .

ولذلك، يمكن اعتبار المصفوفات بمثابة تحويلات خطية للمتجهات. بخاصة التاسع = س, ثور = 0 .

2. معلومات إضافية

2.1. أنظمة المعادلات الخطية

يترك أ- حجم المصفوفة أنا× ج، أ ب- ناقل البعد ج. النظر في المعادلة

الفأس = ب

نسبة إلى المتجه س، أبعاد أنا. في الأساس، هو نظام أناالمعادلات الخطية مع جمجهول س 1 ,...,س ج. الحل موجود إذا وفقط إذا

رتبة( أ) = الرتبة( ب) = ر,

أين بهي مصفوفة موسعة للأبعاد أنا×( ي+1)، تتكون من مصفوفة أ، مكملاً بعمود ب, ب = (أ ب). وإلا فإن المعادلات غير متناسقة.

لو ر = أنا = ج، فالحل فريد

س = أ −1 ب.

لو ر < أنا، فهناك العديد من الحلول المختلفة التي يمكن التعبير عنها من خلال مجموعة خطية ج−رناقلات. نظام المعادلات المتجانسة الفأس = 0 مع مصفوفة مربعة أ (ن× ن) لديه حل غير بديهي ( س ≠ 0 ) إذا وفقط إذا ديت( أ) = 0. إذا ر= الرتبة( أ)<ن، ثم هناك ن−رحلول مستقلة خطيا.

2.2. الأشكال الثنائية والتربيعية

لو أهي مصفوفة مربعة، و سو ذ- متجه البعد المقابل، ثم المنتج القياسي للنموذج سر نعممُسَمًّى خطينالنموذج المحدد بواسطة المصفوفة أ. في س = ذتعبير سر الفأسمُسَمًّى من الدرجة الثانيةاستمارة.

2.3. مصفوفات محددة إيجابية

مصفوفة مربعة أمُسَمًّى إيجابية محددة، إذا كان لأي ناقل غير صفري س ≠ 0 ,

سر الفأس > 0.

تعريف بالمثل سلبي (سر الفأس < 0), غير سلبي (سر الفأس≥ 0) و سلبي (سر الفأس≥ 0) مصفوفات معينة.

2.4. التحلل تشوليسكي

إذا كانت المصفوفة المتماثلة أإيجابية محددة، ثم هناك مصفوفة ثلاثية فريدة من نوعها شمع العناصر الإيجابية، والتي

أ = شر ش.

على سبيل المثال،

أرز. 19 التحلل الكوليسكي

2.5. التحلل القطبي

يترك أهي مصفوفة مربعة غير مفردة البعد ن× ن. ثم هناك فريدة من نوعها القطبيةأداء

أ = ر.س.

أين سهي مصفوفة متماثلة غير سلبية، و رهي مصفوفة متعامدة. المصفوفات سو ريمكن تعريفها بوضوح:

س 2 = أ.أ.ر أو س = (أ.أ.ر) ½ و ر = س −1 أ = (أ.أ.ر) -½ أ.

على سبيل المثال،

أرز. 20 التحلل القطبي

إذا مصفوفة أكان منحطاً، فإن التحلل ليس فريداً - وهو: سما زلت وحيدا، ولكن رربما كثيرا. يمثل التحلل القطبي المصفوفة أكمزيج من الضغط/التمديد سويتحول ر.

2.6. المتجهات الذاتية والقيم الذاتية

يترك أهي مصفوفة مربعة. ناقل ضدمُسَمًّى eigenvectorالمصفوفات أ، لو

شارع = λ ضد,

حيث يتم استدعاء الرقم القيمة الذاتيةالمصفوفات أ. وبالتالي، فإن التحول الذي تقوم به المصفوفة أفوق المتجه ضد، يتلخص في التمدد أو الضغط البسيط بمعامل LA. يتم تحديد المتجه الذاتي حتى الضرب بواسطة ثابت α ≠ 0، أي. لو ضدهو متجه ذاتي، ثم α ضد- أيضًا ناقل ذاتي.

2.7. القيم الذاتية

في المصفوفة أالبعد ( ن× ن) لا يمكن أن يكون أكثر من نالقيم الذاتية. يرضون معادلة مميزة

ديت ( أ − λ أنا) = 0,

وهي معادلة جبرية ن- الترتيب. على وجه الخصوص، بالنسبة للمصفوفة 2×2، تكون المعادلة المميزة بالشكل

على سبيل المثال،

أرز. 21 القيم الذاتية

مجموعة من القيم الذاتية ​​Â 1 ,..., α نالمصفوفات أمُسَمًّى نطاق أ.

الطيف له خصائص مختلفة. بخاصة

ديت ( أ) = lect 1 ×...× lect ن،سب( أ) =  1 +...+ ن.

يمكن أن تكون القيم الذاتية للمصفوفة التعسفية أرقامًا معقدة، ولكن إذا كانت المصفوفة متماثلة ( أر = أ)، فإن قيمها الذاتية حقيقية.

2.8. المتجهات الذاتية

في المصفوفة أالبعد ( ن× ن) لا يمكن أن يكون أكثر من نالمتجهات الذاتية، كل منها يتوافق مع قيمته الذاتية. لتحديد المتجهات الذاتية ضد نالحاجة إلى حل نظام المعادلات المتجانسة

(أ − λ ن أنا)ضد ن = 0 .

لديها حل غير تافه، منذ ديت ( أ -λ ن أنا) = 0.

على سبيل المثال،

أرز. 22 ناقلات ذاتية

المتجهات الذاتية للمصفوفة المتماثلة متعامدة.